Hướng dẫn Giải bài tập Toán 11 Cánh Diều Chương 6 Bài 4 Phương trình, bất phương trình mũ và lôgarit môn Toán học lớp 11 giúp các em học sinh nắm vững phương pháp giải bài tập và ôn luyện tốt kiến thức.
-
Khởi động trang 48 SGK Toán 11 Tập 2 Cánh diều - CD
Dân số được ước tính theo công thức S = A . ert, trong đó A là dân số của năm lấy làm mốc tính, S là dân số sau t năm, r là tỉ lệ tăng dân số hằng năm. Hỏi sau bao nhiêu năm, dân số sẽ gấp đôi dân số của năm lấy làm mốc tính?
-
Hoạt động 1 trang 48 SGK Toán 11 Tập 2 Cánh diều - CD
Trong bài toán ở phần mở đầu, giả sử r = 1,14%/năm.
a) Viết phương trình thể hiện dân số sau t năm gấp đôi dân số ban đầu.
b) Phương trình vừa tìm được có ẩn là gì và nằm ở vị trí nào của luỹ thừa?
-
Luyện tập 1 trang 48 SGK Toán 11 Tập 2 Cánh diều - CD
Cho hai ví dụ về phương trình mũ?
-
Hoạt động 2 trang 48 SGK Toán 11 Tập 2 Cánh diều - CD
a) Vẽ đồ thị hàm số y = 3x và đường thẳng y = 7.
b) Nhận xét về số giao điểm của hai đồ thị trên. Từ đó, hãy nêu nhận xét về số nghiệm của phương trình 3x = 7.
- VIDEOYOMEDIA
-
Luyện tập 2 trang 49 SGK Toán 11 Tập 2 Cánh diều - CD
Giải mỗi phương trình sau:
a) 916 – x = 27x + 4;
b) 16x – 2 = 0,25 . 2–x + 4.
-
Hoạt động 3 trang 49 SGK Toán 11 Tập 2 Cánh diều - CD
Chỉ số thay đổi pH của một dung dịch được tính theo công thức: pH = – log[H+] (trong đó [H+] chỉ nồng độ ion hydrogen). Đo chỉ số pH của một số mẫu nước sông, ta có kết quả là pH = 6,1.
a) Viết phương trình thể hiện nồng độ x của hydrogen [H+] trong mẫu nước sông đó.
b) Phương trình vừa tìm được có ẩn là gì và nằm ở vị trí nào của lôgarit?
-
Luyện tập 3 trang 50 SGK Toán 11 Tập 2 Cánh diều - CD
Cho hai ví dụ về phương trình lôgarit?
-
Hoạt động 4 trang 50 SGK Toán 11 Tập 2 Cánh diều - CD
a) Vẽ đồ thị hàm số y = log4x và đường thẳng y = 5.
b) Nhận xét về số giao điểm của hai đồ thị trên. Từ đó, hãy nêu nhận xét về số nghiệm của phương trình log4x = 5.
-
Luyện tập 4 trang 51 SGK Toán 11 Tập 2 Cánh diều - CD
Giải mỗi phương trình sau:
a)
b) log2x + log4x = 3.
-
Hoạt động 5 trang 51 SGK Toán 11 Tập 2 Cánh diều - CD
Quan sát Hình 11 và nêu nhận xét về tính đồng biến, nghịch biến của hàm số Từ đó, hãy tìm x sao cho
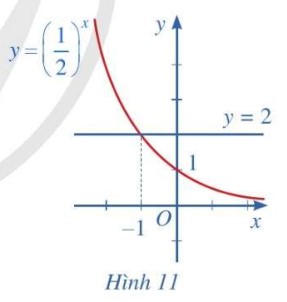
-
Luyện tập 5 trang 52 SGK Toán 11 Tập 2 Cánh diều - CD
Cho hai ví dụ về bất phương trình mũ cơ bản?
-
Luyện tập 6 trang 52 SGK Toán 11 Tập 2 Cánh diều - CD
Giải mỗi bất phương trình sau:
a) 7x+3 < 343;
b)
-
Hoạt động 6 trang 53 SGK Toán 11 Tập 2 Cánh diều - CD
Quan sát Hình 12 và nêu nhận xét về tính đồng biến, nghịch biến của hàm số lôgarit \(y = log_{2}x\). Từ đó, hãy tìm x sao cho \(log_{2}x > 1\)?
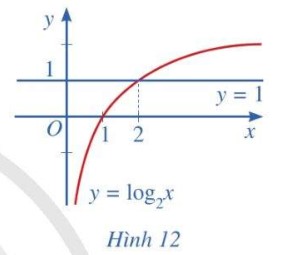
-
Luyện tập 7 trang 53 SGK Toán 11 Tập 2 Cánh diều - CD
Cho hai ví dụ về bất phương trình logarit cơ bản?
-
Luyện tập 8 trang 54 SGK Toán 11 Tập 2 Cánh diều - CD
Giải mỗi bất phương trình sau:
a) log3x < 2;
b)
-
Bài 1 trang 54 SGK Toán 11 Tập 2 Cánh diều - CD
Giải mỗi phương trình sau:
a) (0,3)x–3 = 1;
b) 53x–2 = 25;
c) 9x–2 = 243x+1;
d)
e) log5(3x – 5) = log5(2x + 1);
g)
-
Bài 2 trang 55 SGK Toán 11 Tập 2 Cánh diều - CD
Giải mỗi bất phương trình sau:
a)
b)
c) 4x+3 ≥ 32x;
d) log(x – 1) < 0;
e)
g) ln(x + 3) ≥ ln(2x – 8).
-
Bài 3 trang 55 SGK Toán 11 Tập 2 Cánh diều - CD
Một người gửi ngân hàng 100 triệu đồng theo hình thức lãi kép có kì hạn là 12 tháng với lãi suất x% / năm (x > 0). Sau 3 năm, người đó rút được cả gốc và lãi là 119,1016 triệu đồng. Tìm x, biết rằng lãi suất không thay đổi qua các năm và người đó không rút tiền ra trong suốt quá trình gửi?
-
Bài 4 trang 55 SGK Toán 11 Tập 2 Cánh diều - CD
Sử dụng công thức tính mức cường độ âm L ở Ví dụ 14, hãy tính mức cường độ âm mà tai người có thể chịu đựng được, biết rằng giá trị cực đại của mức cường độ âm mà tai người có thể chịu đựng được là 130dB?
-
Bài tập 53 trang 49 SBT Toán 11 Tập 2 Cánh diều - CD
Nghiệm của phương trình 2x – 1 = 8 là:
A. 2;
B. 4;
C. 3;
D. 5.
-
Bài tập 54 trang 50 SBT Toán 11 Tập 2 Cánh diều - CD
Nghiệm của phương trình 2x = 5 là:
A.
B.
C. x = log25;
D. x = log52.
-
Bài tập 55 trang 50 SBT Toán 11 Tập 2 Cánh diều - CD
Nghiệm của phương trình 92x + 1 = 27x – 3 là:
A. x = – 9;
B. x = 11;
C. x = 9;
D. x = – 11.
-
Bài tập 56 trang 50 SBT Toán 11 Tập 2 Cánh diều - CD
Nghiệm của phương trình log2(x – 5) = 4 là:
A. x = 21;
B. x = 9;
C. x = 13;
D. x = 7.
-
Bài tập 57 trang 50 SBT Toán 11 Tập 2 Cánh diều - CD
Nghiệm của phương trình là:
A. x = 2;
B. x = 5;
C.
D.
-
Bài tập 58 trang 50 SBT Toán 11 Tập 2 Cánh diều - CD
Số nghiệm của phương trình log(x2 – 7x + 12) = log(2x – 8) là:
A. 0;
B. 1;
C. 2;
D. 3.
-
Bài tập 59 trang 50 SBT Toán 11 Tập 2 Cánh diều - CD
Nghiệm của bất phương trình 2x < 5 là:
A. x > log25;
B. x < log52;
C. x < log25;
D. x > log52.
-
Bài tập 60 trang 50 SBT Toán 11 Tập 2 Cánh diều - CD
Tập nghiệm của bất phương trình log0,2(x + 1) > –3 là:
A. (–1; 124);
B. (124; +∞);
C.
D. (–∞; 124).
-
Bài tập 61 trang 50 SBT Toán 11 Tập 2 Cánh diều - CD
Giải mỗi phương trình sau:
a) 3x – 1 = 5;
b)
c)
d) 8x – 2 = 41 – 2x;
e)
g)
-
Bài tập 62 trang 50 SBT Toán 11 Tập 2 Cánh diều - CD
Giải mỗi phương trình sau:
a) log4 (x – 4) = –2;
b) log3 (x2 + 2x) = 1;
c)
d) log9 [(2x – 1)2] = 2;
e) log(x2 – 2x) = log(2x – 3);
g)
-
Bài tập 63 trang 50 SBT Toán 11 Tập 2 Cánh diều - CD
Giải mỗi bất phương trình sau:
a) \({{\left( 0,2 \right)}^{2x+1}}>1;\)
b) \({{27}^{2x}}\le \frac{1}{9};\)
c) \({{\left( \frac{1}{2} \right)}^{{{x}^{2}}-5x+4}}\ge 4;\)
d) \({{\left( \frac{1}{25} \right)}^{x+1}}<{{125}^{2x}};\)
e) \({{\left( \sqrt{2}-1 \right)}^{3x-2}}<{{\left( \sqrt{2}+1 \right)}^{4-x}};\)
g) \({{\left( 0,5 \right)}^{2{{x}^{2}}-x}}>{{\left( \sqrt{2} \right)}^{4x-12}}.\)
-
Bài tập 64 trang 51 SBT Toán 11 Tập 2 Cánh diều - CD
Giải mỗi bất phương trình sau:
a)
b) log3 (x2 – 2x + 2) > 0;
c)
d) log0,5 (x – 1) ≥ log0,5 (5 – 2x);
e) log(x2 + 1) ≤ log(x + 3);
g)
-
Bài tập 65 trang 51 SBT Toán 11 Tập 2 Cánh diều - CD
Người ta nuôi cấy vi khuẩn Bacillus subtilis trong nồi lên men và thu được số liệu sau: Lúc ban đầu, số tế bào/1 ml dịch nuôi là 2.102. Sau 13 giờ, số tế bào/1 ml dịch nuôi là 3,33.109. Biết vi khuẩn Bacillus subtilis sinh trưởng trong điều kiện tối ưu và sinh sản theo hình thức tự nhân đôi. Hỏi sau bao nhiêu phút, vi khuẩn Bacillus subtilis tự nhân đôi một lần (làm tròn kết quả đến hàng đơn vị)?
-
Bài tập 66 trang 51 SBT Toán 11 Tập 2 Cánh diều - CD
Tốc độ của gió S (dặm/giờ) gần tâm của một con lốc xoáy được tính bởi công thức S = 93logd + 65, trong đó d (dặm) là quãng đường cơn lốc xoáy đó di chuyển được. Tính quãng đường cơn lốc xoáy đã di chuyển được, biết tốc độ của gió ở gần tâm bằng 140 dặm/giờ (làm tròn kết quả đến hàng phần mười)?
-
Bài tập 67 trang 51 SBT Toán 11 Tập 2 Cánh diều - CD
Dân số thành phố Hà Nội năm 2022 khoảng 8,4 triệu người. Giả sử tỉ lệ tăng dân số hằng năm của Hà Nội không đổi và bằng r = 1,04%. Biết rằng, sau t năm dân số Hà Nội (tính từ mốc năm 2022) ước tính theo công thức: S = A . ert, trong đó A là dân số năm lấy làm mốc. Hỏi từ năm nào trở đi, dân số Hà Nội vượt quá 10 triệu người?
-
Bài tập 68 trang 51 SBT Toán 11 Tập 2 Cánh diều - CD
Mức cường độ âm L (dB) được tính bởi công thức trong đó I (W/m2) là cường độ âm. Để đảm bảo sức khỏe cho công nhân, mức cường độ âm trong một nhà máy phải giữ sao cho không vượt quá 85 dB. Hỏi cường độ âm của nhà máy đó phải thỏa mãn điều kiện nào để đảm bảo sức khỏe cho công nhân?


