Bài tập 2 trang 24 SGK Hình học 11

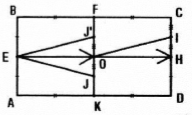
Xét phép đối xứng trục Đ_EH ta có:

F = Đ_EH (K), B = Đ_EH (B), E = Đ_EH(E), Đ_EH (J) = J' (J' là trung điểm OF).

Vậy ảnh của hình thang AEJK qua Đ_EH là hình thang BEJ'F (1).

Xét phép tịnh tiến \({T_{\overrightarrow {EO} }}\) ta có \(F = {T_{\overrightarrow {EO} }}(B),\,I = {T_{\overrightarrow {EO} }}(J'),\,C = {T_{\overrightarrow {EO} }}(F),O = {T_{\overrightarrow {EO} }}(E).\)

Vậy hình thang FOIC là ảnh của hình thang BEJ'F qua  \({T_{\overrightarrow {EO} }}\) (2).

Từ (1) và (2) ta có tồn tại phép dời hình (thực hiện liên tiếp hai phép dời hình là đối xứng trục và tịnh tiến ta cũng được một phép dời hình) biến hình thang AEJK thành hình thang FOIC hay hai hình thang đó bằng nhau.

-- Mod Toán 11 HỌC247