Bài tập 23 trang 23 SGK Hình học 11 NC
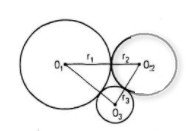
Hình H1 gồm ba đường tròn (O1; r1),(O2; r2) và (O3; r3) đôi một tiếp xúc ngoài với nhau. Hình H2 gồm ba đường tròn (I1; r1),(I2; r2) và (I3; r3) đôi một tiếp xúc ngoài với nhau. Chứng tỏ rằng hai hình H1 và H2 bằng nhau = r.
Hướng dẫn giải chi tiết
\(\begin{array}{l}
{O_1}{O_2} = {r_1} + {r_2} = {I_1}{I_2}\\
{O_2}{O_3} = {r_2} + {r_3} = {I_2}{I_3}\\
{O_3}{O_1} = {r_3} + {r_1} = {I_3}{I_1}
\end{array}\)
\( \Rightarrow {\rm{\Delta }}{O_1}{O_2}{O_3} = {\rm{\Delta }}{I_1}{I_2}{I_3}\)
Nên có phép dời hình F biến ba điểm O1, O2, O3 lần lượt thành ba điểm I1, I2, I3
Hiển nhiên khi đó F biến ba đường tròn \(({O_1};{r_1}),({O_2};{r_2}),({O_3};{r_3})\) lần lượt thành ba đường tròn \(({I_1};{r_1}),({I_2};{r_2}),({I_3};{r_3})\), tức là biến hình H1 thành hình H2
Vậy hai hình H1 và H2 bằng nhau.
-- Mod Toán 11 HỌC247
Bài tập SGK khác
-


Cho phép vị tự tâm Obieens M thành N sao cho OM=3 ON .Khi đó tỉ số vị tự là ?
Theo dõi (0) 2 Trả lời



