Hôm nay chúng ta sẽ khám phá một chủ đề toán học thú vị cùng HOC247 về Hai đường thẳng song song trong không gian của chương 4 Toán 11 Cánh Diều. Thông qua bài học này, các em sẽ tìm hiểu về vị trí hai đường thẳng song song và các tính chất của chúng. Chúc các em học tập thật tốt!
Tóm tắt lý thuyết
1.1. Vị trí tương đối của hai đường thẳng phân biệt
Nhận xét:
- Cho hai đường thẳng a và b phân biệt trong không gian. Khi đó chỉ xảy ra một trong các trường hợp sau:
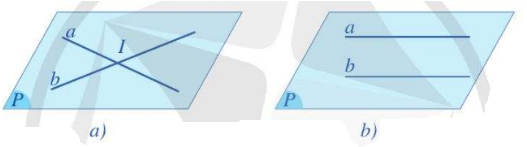
+ Trường hợp 1: Có một mặt phẳng chứa a và b. Khi đó ta nói a và b đồng phẳng (Hình a).
+ Trường hợp 2: Không có mặt phẳng nào chứa a và b. Khi đó ta nói a và b chéo nhau, hay a chéo với b (Hình b).

+ a và b có một điểm chung duy nhất I. Ta nói a và b cắt nhau tại I và kí hiệu là a ∩ b = {I}. Ta còn có thể viết a ∩ b = I (Hình a).
+ a và b không có điểm chung. Ta nói a và b song song với nhau, kí hiệu là a // b (Hình b).
| Khái niệm: Hai đường thẳng song song là hai đường thẳng cùng nằm trong một mặt phẳng và không có điểm chung. |
Nhận xét: Cho hai đường thẳng song song a và b. Có duy nhất một mặt phẳng chứa hai đường thẳng đó, kí hiệu là mp(a, b).
1.2. Tính chất
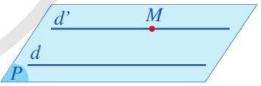
| Định lí 1: Trong không gian, qua một điểm không nằm trên đường thẳng cho trước, có một và chỉ một đường thẳng song song với đường thẳng đã cho. |
- Tức là, trong không gian, cho điểm M và đường thẳng d không đi qua M. Có một và chỉ một đường thẳng d’ đi qua điểm M và song song với đường thẳng d.
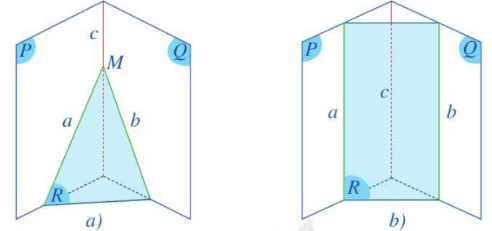
| Định lí 2 (về giao tuyến của ba mặt phẳng): Nếu ba mặt phẳng đôi một cắt nhau theo ba giao tuyến phân biệt thì ba giao tuyến ấy hoặc đồng quy, hoặc đôi một song song với nhau. |
- Tức là, trong không gian, cho ba mặt phẳng (P), (Q), (R) đôi một cắt nhau theo ba giao tuyến phân biệt a, b, c, trong đó a = (P) ∩ (R), b = (R) ∩ (Q), c = (Q) ∩ (P).
- Khi đó ta có hai khả năng xảy ra như sau:
+ Trường hợp 1: Ba giao tuyến a, b, c đồng quy tại M (Hình a).
+ Trường hợp 2: Ba giao tuyến a, b, c song song với nhau (Hình b).
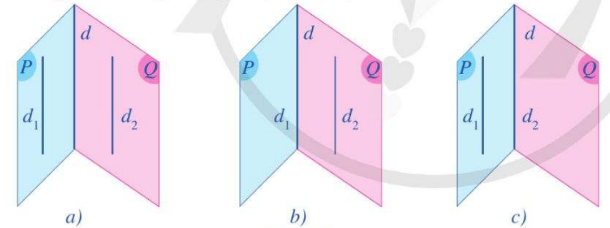
Hệ quả: Nếu hai mặt phẳng phân biệt lần lượt chứa hai đường thẳng song song thì giao tuyến của chúng (nếu có) cũng song song với hai đường thẳng đó hoặc trùng với một trong hai đường thẳng đó.
| Định lí 3: Trong không gian, hai đường thẳng phân biệt cùng song song với đường thẳng thứ ba thì song song với nhau. |
- Khi hai đường thẳng a và b cùng song song với đường thẳng c, ta kí hiệu a // b // c và gọi là ba đường thẳng song song.
Bài tập minh họa
Cho hình chóp S.ABCD có đáy ABCD là hình thang (đáy lớn AB, đáy nhỏ CD). Gọi M, N lần lượt là trung điểm của SA và SB. Gọi P là giao điểm của SC và (AND). Gọi I là giao điểm của AN và DP. Hỏi tứ giác SABI là hình gì?
Hướng dẫn giải
.png)
- Trong (ABCD): gọi E = AD ∩ BC.
Mà AD ⊂ (AND) và BC ⊂ (SBC).
Suy ra E ∈ (AND) và E ∈ (SBC).
- Trong (SBC): gọi P = SC ∩ NE.
Mà NE ⊂ (AND).
Vì vậy P là giao điểm của đường thẳng SC và mặt phẳng (AND).
- Ta có I = AN ∩ DP.
Mà AN ⊂ (SAB) và DP ⊂ (SCD).
Suy ra I cùng thuộc hai mặt phẳng (SAB) và (SCD).
Mà S cùng thuộc hai mặt phẳng (SAB) và (SCD).
Do đó SI = (SAB) ∩ (SCD).
Lại có AB = (SAB) ∩ (ABCD) và CD = (SCD) ∩ (ABCD).
Mà trong (ABCD), ta lại có AB // CD (do ABCD là hình thang với đáy lớn AB, đáy nhỏ CD).
Do đó SI // AB // CD.
- Tam giác SAB có M, N lần lượt là trung điểm của SA, SB.
Suy ra MN là đường trung bình của tam giác SAB.
Do đó MN // AB.
Vì vậy MN // SI (do AB // SI).
Mà N là trung điểm SA.
Do đó M là trung điểm AI.
- Tứ giác SABI có hai đường chéo SB và AI cắt nhau tại trung điểm M của mỗi đường.
Vậy tứ giác SABI là hình bình hành.
3. Luyện tập Bài 2 Chương 4 Toán 11 Cánh Diều
Học xong bài học này, em có thể:
- Nhận biết quan hệ song song giữa các đường thẳng.
- Vận dụng được các tính chất về quan hệ song song giữa các đường thẳng.
3.1. Trắc nghiệm Bài 2 Chương 4 Toán 11 Cánh Diều
Các em có thể hệ thống lại nội dung kiến thức đã học được thông qua bài kiểm tra Trắc nghiệm Toán 11 Cánh Diều Bài 2 cực hay có đáp án và lời giải chi tiết.
-
- A. 5
- B. 3
- C. 1
- D. 2
-
Câu 2:
Cho hình chóp \(S.ABCD\) với đáy là tứ giác \(ABCD\) có các cạnh đối không song song. Giả sử \(AC\cap BD=O\), \(AD\cap BC=I\). Giao tuyến của hai mp \(\left( SAC \right)\) và \(\left( SBD \right)\) là?
- A. \(SC\).
- B. \(SB\).
- C. \(SO\).
- D. \(SI\).
-
- A. \(d\) qua \(S\) và song song với \(CD\).
- B. \(d\) qua \(S\) và song song với \(BC\).
- C. \(d\) qua \(S\) và song song với \(BD\).
- D. \(d\) qua \(S\) và song song với \(AB\).
Câu 4-10: Mời các em đăng nhập xem tiếp nội dung và thi thử Online để củng cố kiến thức về bài học này nhé!
3.2. Bài tập SGK Bài 2 Chương 4 Toán 11 Cánh Diều
Các em có thể xem thêm phần hướng dẫn Giải bài tập Toán 11 Cánh Diều Bài 2 để giúp các em nắm vững bài học và các phương pháp giải bài tập.
Khởi động trang 95 SGK Toán 11 Cánh diều Tập 1 - CD
Hoạt động 1 trang 95 SGK Toán 11 Cánh diều Tập 1 - CD
Luyện tập 1 trang 97 SGK Toán 11 Cánh diều Tập 1 - CD
Hoạt động 2 trang 97 SGK Toán 11 Cánh diều Tập 1 - CD
Hoạt động 3 trang 97 SGK Toán 11 Cánh diều Tập 1 - CD
Luyện tập 2 trang 99 SGK Toán 11 Cánh diều Tập 1 - CD
Hoạt động 4 trang 99 SGK Toán 11 Cánh diều Tập 1 - CD
Luyện tập 3 trang 100 SGK Toán 11 Cánh diều Tập 1 - CD
Bài 1 trang 100 SGK Toán 11 Cánh diều Tập 1 - CD
Bài 2 trang 100 SGK Toán 11 Cánh diều Tập 1 - CD
Bài 3 trang 100 SGK Toán 11 Cánh diều Tập 1 - CD
Bài 4 trang 100 SGK Toán 11 Cánh diều Tập 1 - CD
Bài 5 trang 100 SGK Toán 11 Cánh diều Tập 1 - CD
Bài 6 trang 100 SGK Toán 11 Cánh diều Tập 1 - CD
Bài 7 trang 100 SGK Toán 11 Cánh diều Tập 1 - CD
Bài tập 10 trang 99 SBT Toán 11 Tập 1 Cánh diều - CD
Bài tập 11 trang 99 SBT Toán 11 Tập 1 Cánh diều - CD
Bài tập 12 trang 100 SBT Toán 11 Tập 1 Cánh diều - CD
Bài tập 13 trang 100 SBT Toán 11 Tập 1 Cánh diều - CD
Bài tập 14 trang 100 SBT Toán 11 Tập 1 Cánh diều - CD
Bài tập 15 trang 100 SBT Toán 11 Tập 1 Cánh diều - CD
Bài tập 16 trang 100 SBT Toán 11 Tập 1 Cánh diều - CD
Bài tập 17 trang 100 SBT Toán 11 Tập 1 Cánh diều - CD
Bài tập 18 trang 100 SBT Toán 11 Tập 1 Cánh diều - CD
4. Hỏi đáp Bài 2 Chương 4 Toán 11 Cánh Diều
Trong quá trình học tập nếu có thắc mắc hay cần trợ giúp gì thì các em hãy comment ở mục Hỏi đáp, Cộng đồng Toán học HOC247 sẽ hỗ trợ cho các em một cách nhanh chóng!
Chúc các em học tập tốt và luôn đạt thành tích cao trong học tập!
-- Mod Toán Học 11 HỌC247










