Hiểu rõ việc tóm tắt kiến thức sau mỗi bài học giúp các em hệ thống kiến thức một cách nhanh chóng và hiệu quả. HOC247 đã biên soạn Tóm tắt lý thuyết Bài Hàm số liên tục môn Toán lớp 11 sách Kết Nối Tri Thức. Ngoài ra, các em cũng có thể tham khảo các Bài tập minh họa phía dưới bài học này. Từ đó nắm vững các phương pháp giải các dạng toán của Bài Hàm số liên tục. Chúc các em học tập thật hiệu quả!
Tóm tắt lý thuyết
1.1. Hàm số liên tục tại một điểm
|
Cho hàm số \(y = f(x)\) xác định trên khoảng (a;b) và \({x_0} \in (a;b)\). - Hàm số \(y = f(x)\) liên tục tại \({x_0} \Leftrightarrow \mathop {\lim }\limits_{x \to {x_0}} f(x) = f({x_0})\). - Hàm số \(y = f(x)\) không liên tục tại \({x_0}\) ta nói hàm số gián đoạn tại \({x_0}\). |
1.2. Hàm số liên tục trên một khoảng
|
- \(y = f(x)\) liên tục trên một khoảng nếu nó kiên tục tại mọi điểm của khoảng đó - \(y = f(x)\) liên tục trên đoạn \(\left[ {a;b} \right]\) nếu nó liên tục trên \(\left( {a;b} \right)\) và \(\mathop {\lim }\limits_{x \to {a^ + }} f(x) = f(a)\), \(\mathop {\lim }\limits_{x \to {b^ - }} f(x) = f(b)\) |
+ Hàm số đa thức liên tục trên tập R.
+ Hàm số phân thức hữu tỉ và hàm số lượng giác liên tục trên từng khoảng xác định của chúng.
1.3. Một số tính chất cơ bản
Các hàm số \(y = f(x),{\rm{ }}y = g(x)\) liên tục tại \({x_0}\). Khi đó tổng, hiệu, tích liên tục tai x0, thương \(y = \frac{{f(x)}}{{g(x)}}\) liên tục nếu \(g({x_0}) \ne 0\).
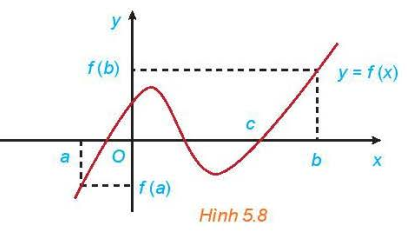
Nhận xét: Cho hàm số f liên tục trên đoạn \(\left[ {a;b} \right]\). Nếu \(f(a){\rm{ }}f(b) < 0\) thì tồn tại ít nhất một số \(c \in \left( {a;b} \right)\) sao cho \(f(c) = 0\).
Bài tập minh họa
Vấn đề 1: Xét tính liên tục của hàm số tại một điểm
- Phương pháp:
+ Tìm giới hạn của hàm số \(y = f(x)\) khi \(x \to {x_0}\) và tính \(f({x_0})\)
+ Nếu tồn tại \(\mathop {\lim }\limits_{x \to {x_0}} f(x)\) thì ta so sánh \(\mathop {\lim }\limits_{x \to {x_0}} f(x)\) với \(f({x_0})\).
Ví dụ 1:
Xét tính liên tục của hàm số sau tại \(x = 3\)
a) \(f\left( x \right) = \left\{ {\begin{array}{*{20}{c}}{\frac{{{x^3} - 27}}{{{x^2} - x - 6}}\,\,\,{\rm{khi}}\,x \ne 3}\\{\frac{{10}}{3}\,\,\,{\rm{ khi}}\,\,x = 3}\end{array}} \right.\)
b) \(f\left( x \right) = \left\{ {\begin{array}{*{20}{c}}{\frac{{x - 3}}{{\sqrt {2x + 3} - 3}}\,\,\,{\rm{khi }}\,x < 3}\\{\,\,{{\left( {x - 1} \right)}^2}\,\,\,\,\,\,\,\,\,{\rm{khi }}\,\,x \ge 3}\end{array}} \right.\)
Hướng dẫn giải
a) Hàm số xác định trên \(\mathbb{R}\)
Ta có \(f(3) = \frac{{10}}{3}\) và \(\mathop {\lim }\limits_{x \to 3} f(x) = \mathop {\lim }\limits_{x \to 3} \frac{{{x^3} - 27}}{{{x^2} - x - 6}} = \mathop {\lim }\limits_{x \to 3} \frac{{(x - 3)({x^2} + 3x + 9)}}{{(x - 3)(x + 2)}}\)
\( = \mathop {\lim }\limits_{x \to 3} \frac{{{x^2} + 3x + 9}}{{x + 2}} = \frac{{27}}{5} \ne f(3)\).
Vậy hàm số không liên tục tại \(x = 3\).
b) Ta có \(f(3) = 4\) và \(\mathop {\lim }\limits_{x \to {3^ + }} f(x) = \mathop {\lim }\limits_{x \to {3^ + }} {(x - 1)^2} = 4\) ; \(\mathop {\lim }\limits_{x \to {3^ - }} f(x) = \mathop {\lim }\limits_{x \to {3^ - }} \frac{{x - 3}}{{\sqrt {2x + 3} - 3}} = \mathop {\lim }\limits_{x \to {3^ - }} \frac{{\sqrt {2x + 3} + 3}}{2} = 3 \ne \mathop {\lim }\limits_{x \to {3^ + }} f(x)\)
Vậy hàm số gián đoạn tại \(x = 3\).
Vấn đề 2: Xét tính liên tục của hàm số trên một tập
- Phương pháp: Sử dụng các định lí về tính liên tục của hàm đa thức, lương giác, phân thức hữu tỉ …
- Nếu hàm số cho dưới dạng nhiều công thức thì ta xét tính liên tục trên mỗi khoảng đã chia và tại các điểm chia của các khoảng đó.
Ví dụ 1:
Xét tính liên tục của các hàm số sau trên toàn trục số:
a) \(f(x) = \tan 2x + \cos x\)
b) \(f(x) = \frac{{\sqrt {x - 1} + 2}}{{{x^2} - 3x + 2}}\)
Hướng dẫn giải
a) TXĐ: \(D = \mathbb{R}\backslash \left\{ {\frac{\pi }{4} + k\frac{\pi }{2},k \in \mathbb{Z}} \right\}\)
Vậy hàm số liên tục trên \(D\)
b) Điều kiện xác định: \(\left\{ \begin{array}{l}x - 1 \ge 0\\{x^2} - 3x + 2 \ne 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x > 1\\x \ne 2\end{array} \right.\)
Vậy hàm số liên tục trên \(\left( {1;2} \right) \cup \left( {2; + \infty } \right)\).
Vấn đề 3: Chứng minh phương trình có nghiệm
Phương pháp:
Để chứng minh phương trình \(f(x) = 0\) có ít nhất một nghiệm trên D, ta chứng minh hàm số \(y = f(x)\) liên tục trên D và có hai số \(a,b \in D\) sao cho \(f(a).f(b) < 0\).
Để chứng minh phương trình \(f(x) = 0\) có k nghiệm trên D, ta chứng minh hàm số \(y = f(x)\) liên tục trên D và tồn tại k khoảng rời nhau \(({a_i};{a_{i + 1}})\) (i=1,2,…,k) nằm trong D sao cho \(f({a_i}).f({a_{i + 1}}) < 0\).
Ví dụ 1:
Chứng minh rằng phương trình sau có ít nhất một nghiệm :
a) \({x^7} + 3{x^5} - 1 = 0\)
b) \({x^2}\sin x + x\cos x + 1 = 0\)
Hướng dẫn giải
a) Ta có hàm số \(f(x) = {x^7} + 3{x^5} - 1\) liên tục trên R và \(f(0).f(1) = - 3 < 0\)
Suy ra phương trinh \(f(x) = 0\) có ít nhất một nghiệm thuộc \((0;1)\).
b) Ta có hàm số \(f(x) = {x^2}\sin x + x\cos x + 1\) liên tục trên R và \(f(0).f(\pi ) = - \pi < 0\). Suy ra phương trinh \(f(x) = 0\) có ít nhất một nghiệm thuộc \((0;\pi )\).
Luyện tập Bài 17 Toán 11 Kết Nối Tri Thức
Học xong bài học này, em có thể:
- Nhận dạng hàm số liên tục tại một điểm, hoặc trên một khoảng/đoạn. Nhận dạng tính liên tục của tổng, hiệu, tích, thương của hai hàm số liên tục.
- Nhận biết tính liên tục của một số hàm sơ cấp cơ bản trên tập xác định của chúng.
3.1. Trắc nghiệm Bài 17 Toán 11 Kết Nối Tri Thức
Các em có thể hệ thống lại nội dung kiến thức đã học được thông qua bài kiểm tra Trắc nghiệm Toán 11 Kết nối tri thức Chương 5 Bài 17 cực hay có đáp án và lời giải chi tiết.
-
- A. Hàm số \(f\left( x \right)\) xác định trên \(\left( a;b \right)\) được gọi là liên tục tại \({{x}_{0}}\in \left( a;b \right)\) nếu \(\underset{x\to {{x}_{0}}^{+}}{\mathop{\lim }}\,f\left( x \right)=\underset{x\to {{x}_{0}}^{-}}{\mathop{\lim }}\,f\left( x \right)=f\left( {{x}_{0}} \right)\).
- B. Nếu hàm số \(f\left( x \right)\) liên tục trên \(\left[ a;b \right]\) thì \(f\left( x \right)\) đạt giá trị nhỏ nhất, giá trị lớn nhất trên \(\left[ a;b \right]\).
- C. Nếu hàm số \(f\left( x \right)\) liên tục trên \(\left[ a;b \right]\) và \(f\left( a \right).f\left( b \right)>0\) thì phương trình \(f\left( x \right)=0\) không có nghiệm trên \(\left( a;b \right)\).
- D. Các hàm đa thức, hàm lượng giác liên tục tại mọi điểm mà nó xác định.
-
- A. \(a=1\).
- B. \(a=-1\).
- C. \(a=-\frac{1}{4}\).
- D. \(a=\frac{1}{4}\).
-
- A. \(m=0\).
- B. \(m=2\).
- C. \(m=1\).
- D. \(m=3\).
Câu 4-10: Mời các em đăng nhập xem tiếp nội dung và thi thử Online để củng cố kiến thức về bài học này nhé!
3.2. Bài tập SGK Bài 17 Toán 11 Kết Nối Tri Thức
Các em có thể xem thêm phần hướng dẫn Giải bài tập Toán 11 Kết nối tri thức Chương 5 Bài 17 để giúp các em nắm vững bài học và các phương pháp giải bài tập.
Mở đầu trang 119 SGK Toán 11 Kết nối tri thức tập 1 - KNTT
Hoạt động 1 trang 119 SGK Toán 11 Kết nối tri thức tập 1 - KNTT
Luyện tập 1 trang 120 SGK Toán 11 Kết nối tri thức tập 1 - KNTT
Hoạt động 2 trang 120 SGK Toán 11 Kết nối tri thức tập 1 - KNTT
Luyện tập 2 trang 121 SGK Toán 11 Kết nối tri thức tập 1 - KNTT
Hoạt động 3 trang 121 SGK Toán 11 Kết nối tri thức tập 1 - KNTT
Giải Bài 5.14 trang 122 SGK Toán 11 Kết nối tri thức tập 1 - KNTT
Giải Bài 5.15 trang 122 SGK Toán 11 Kết nối tri thức tập 1 - KNTT
Giải Bài 5.16 trang 122 SGK Toán 11 Kết nối tri thức tập 1 - KNTT
Giải Bài 5.17 trang 122 SGK Toán 11 Kết nối tri thức tập 1 - KNTT
Bài tập 5.21 trang 86 SBT Toán 11 Tập 1 Kết nối tri thức - KNTT
Bài tập 5.22 trang 86 SBT Toán 11 Tập 1 Kết nối tri thức - KNTT
Bài tập 5.23 trang 86 SBT Toán 11 Tập 1 Kết nối tri thức - KNTT
Bài tập 5.24 trang 86 SBT Toán 11 Tập 1 Kết nối tri thức - KNTT
Bài tập 5.25 trang 86 SBT Toán 11 Tập 1 Kết nối tri thức - KNTT
Hỏi đáp Bài 17 Toán 11 Kết Nối Tri Thức
Trong quá trình học tập nếu có thắc mắc hay cần trợ giúp gì thì các em hãy comment ở mục Hỏi đáp, Cộng đồng Toán học HOC247 sẽ hỗ trợ cho các em một cách nhanh chóng!
Chúc các em học tập tốt và luôn đạt thành tích cao trong học tập!
-- Mod Toán Học 11 HỌC247