Bài 2 trang 99 SGK Toán 11 Tập 2 Cánh diều - CD

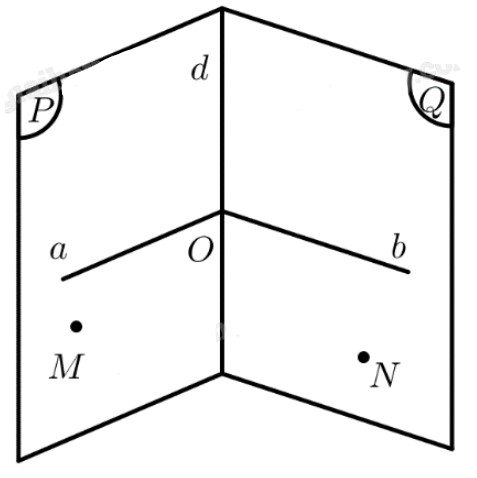
Cho hai mặt phẳng \(\left( P \right),\left( Q \right)\) vuông góc với nhau. Ta cần chứng minh tồn tại một đường thẳng \(a \subset \left( P \right)\) sao cho \(a \bot \left( Q \right)\).

Gọi \(d = \left( P \right) \cap \left( Q \right)\). Lấy \(M \in \left( P \right),N \in \left( Q \right)\) sao cho \(M,N \notin d\).

Gọi góc \(\widehat {aOb}\) là góc phẳng nhị diện của góc nhị diện \(\left[ {M,d,N} \right]\).

Vì \(\left( P \right) \bot \left( Q \right)\) nên góc nhị diện đó là góc nhị diện vuông. Vậy \(\widehat {aOb} = {90^ \circ } \Rightarrow a \bot b\).

Mà \(a \bot d\)

\( \Rightarrow a \bot \left( Q \right)\)

-- Mod Toán 11 HỌC247