Bài tập 39 trang 104 SBT Toán 11 Tập 2 Cánh diều - CD

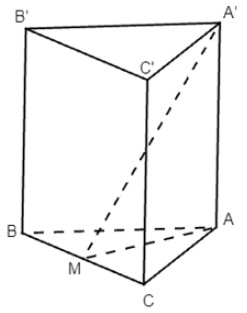
Vì tam giác ABC cân tại A, AM là đường trung tuyến nên AM ⊥ BC.

Ta có: AA’ ⊥ (ABC), AA’ // BB’, suy ra BB’ ⊥ (ABC).

Mà AM ⊂ (ABC) nên BB’ ⊥ AM.

Ta có: AM ⊥ BC, AM ⊥ BB’, BC ∩ BB’ = B trong (BCC’B’).

Từ đó suy ra AM ⊥ (BCC’B’).

Mà AM ⊂ (MAA’) nên (MAA’) ⊥ (BCC’B’).

-- Mod Toán 11 HỌC247