Bài tập 41 trang 104 SBT Toán 11 Tập 2 Cánh diều - CD

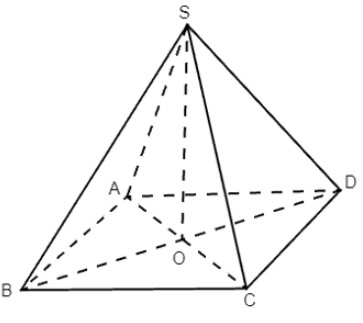
Gọi O là giao điểm của AC và BD.

Suy ra: O ∈ AC ⊂ (SAC) và O ∈  BD ⊂ (SBD) nên O ∈ (SAC) ∩ (SBD).

Hơn nữa S ∈ (SAC) ∩ (SBD).

Nên SO = (SAC) ∩ (SBD).

Vì (SAC) ⊥ (ABCD), (SBD) ⊥ (ABCD) và SO = (SAC) ∩ (SBD), ta suy ra SO ⊥ (ABCD).

Mà AC ⊂ (ABCD) nên SO ⊥ AC.

Do ABCD là hình thoi, nên AC ⊥ BD.

Ta có: AC ⊥ SO, AC ⊥ BD và SO ∩ BD = O trong (SBD).

Suy ra AC ⊥ (SBD).

Mặt khác AC ⊂ (SAC).

Từ đó ta có: (SAC) ⊥ (SBD).

-- Mod Toán 11 HỌC247