Bài 5 trang 99 SGK Toán 11 Tập 2 Cánh diều

Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình chữ nhật, mặt phẳng \(\left( {SAB} \right)\) vuông góc với mặt đáy, tam giác \(SAB\) vuông cân tại \(S\). Gọi \(M\) là trung điểm của \(AB\). Chứng minh rằng:

a) \(SM \bot \left( {ABCD} \right)\);

b) \(AD \bot \left( {SAB} \right)\);

c) \(\left( {SAD} \right) \bot \left( {SBC} \right)\).

QUẢNG CÁO

Hướng dẫn giải chi tiết Bài 5

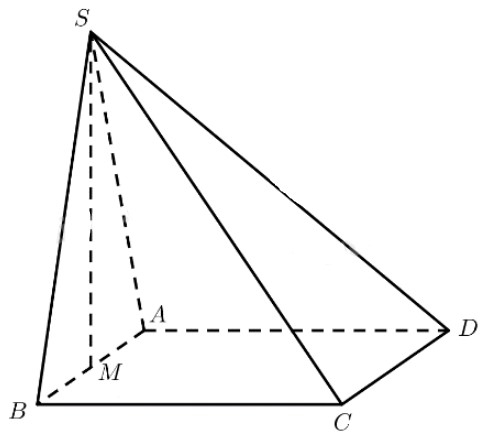
a) Tam giác \(SAB\) vuông cân tại \(S\), có \(M\) là trung điểm của \(AB\)

\(\left. \begin{array}{l} \Rightarrow SM \bot AB\\\left( {SAB} \right) \bot \left( {ABCD} \right)\\\left( {SAB} \right) \cap \left( {ABCD} \right) = AB\end{array} \right\} \Rightarrow SM \bot \left( {ABCD} \right)\)

b) Ta có: \(ABCD\) là hình chữ nhật \( \Rightarrow AB \bot A{\rm{D}}\)

\(SM \bot \left( {ABCD} \right) \Rightarrow SM \bot A{\rm{D}}\)

\( \Rightarrow A{\rm{D}} \bot \left( {SAB} \right)\)

c) Ta có: \(A{\rm{D}} \bot \left( {SAB} \right) \Rightarrow A{\rm{D}} \bot SB\)

Tam giác \(SAB\) vuông cân tại \(S\)\( \Rightarrow SA \bot SB\)

\(\left. \begin{array}{l} \Rightarrow SB \bot \left( {SA{\rm{D}}} \right)\\SB \subset \left( {SBC} \right)\end{array} \right\} \Rightarrow \left( {SBC} \right) \bot \left( {SA{\rm{D}}} \right)\)

Tam giác \(SAB\) vuông cân tại \(S\), có \(M\) là trung điểm của \(AB\)

-- Mod Toán 11 HỌC247

Nếu bạn thấy hướng dẫn giải Bài 5 trang 99 SGK Toán 11 Tập 2 Cánh diều - CD HAY thì click chia sẻ