Giải bài tập SGK Bài 4 Chương 4 Toán 10 Cơ bản & Nâng cao

Biểu diễn hình học tập nghiệm của các bất phương trình bậc nhất hai ẩn sau:

a) \(- x + 2 + 2(y - 2) < 2(1 - x);\)

b) \(3(x - 1) + 4(y - 2) < 5x - 3.\)

 Biểu diễn hình học tập nghiệm của các hệ bất phương trình hai ẩn sau.

a) \(\left\{\begin{matrix} x-2y<0\\ x+3y>-2 \\ y-x<3; \end{matrix}\right.\)

b) \(\left\{\begin{matrix} \frac{x}{3}+\frac{y}{2}-1<0\\ x+\frac{1}{2}-\frac{3y}{2}\leq 2 \\ x\geq 0. \end{matrix}\right.\)

Có ba nhóm máy A, B, C dùng để sản xuất ra hai loại sản phẩm I và II. Để sản xuất một đơn vị sản phẩm mỗi loại phải lần lượt dùng các máy thuộc các nhóm khác nhau. Số máy trong một nhóm và số máy của từng nhóm cần thiết để sản xuất ra một đơn vị sản phẩm thuộc mỗi loại được cho trong bảng sau:

Một đơn vị sản phẩm I lãi 3 nghìn đồng, một sản phẩm II lãi 5 nghìn đồng. Hãy lập phương án để việc sản xuất hai loại sản phẩm trên có lãi cao nhất.

Biểu diễn hình học tập nghiệm của các bất phương trình sau:

a) 3 + 2y > 0;                 b) 2x - 1 < 0;

c) x - 5y < 2;                  d) 2x + y > 1;

e) -3x + y + 2 ≤ 0;          e) 2x - 3y + 5 ≥ 0.

Một hộ nông dân trồng đậu và cà trên diện tích 8a. Nếu trồng đậu thì cần 20 công và thu 3 000 000 đồng trên một a, nếu trồng cà thì cần 30 công và thu 40 000 000 đồng trên một a. Hỏi cần trồng mỗi loại cây trên diện tích là bao nhiêu để thu được nhiều tiền nhất khi tổng số công không quá 180?

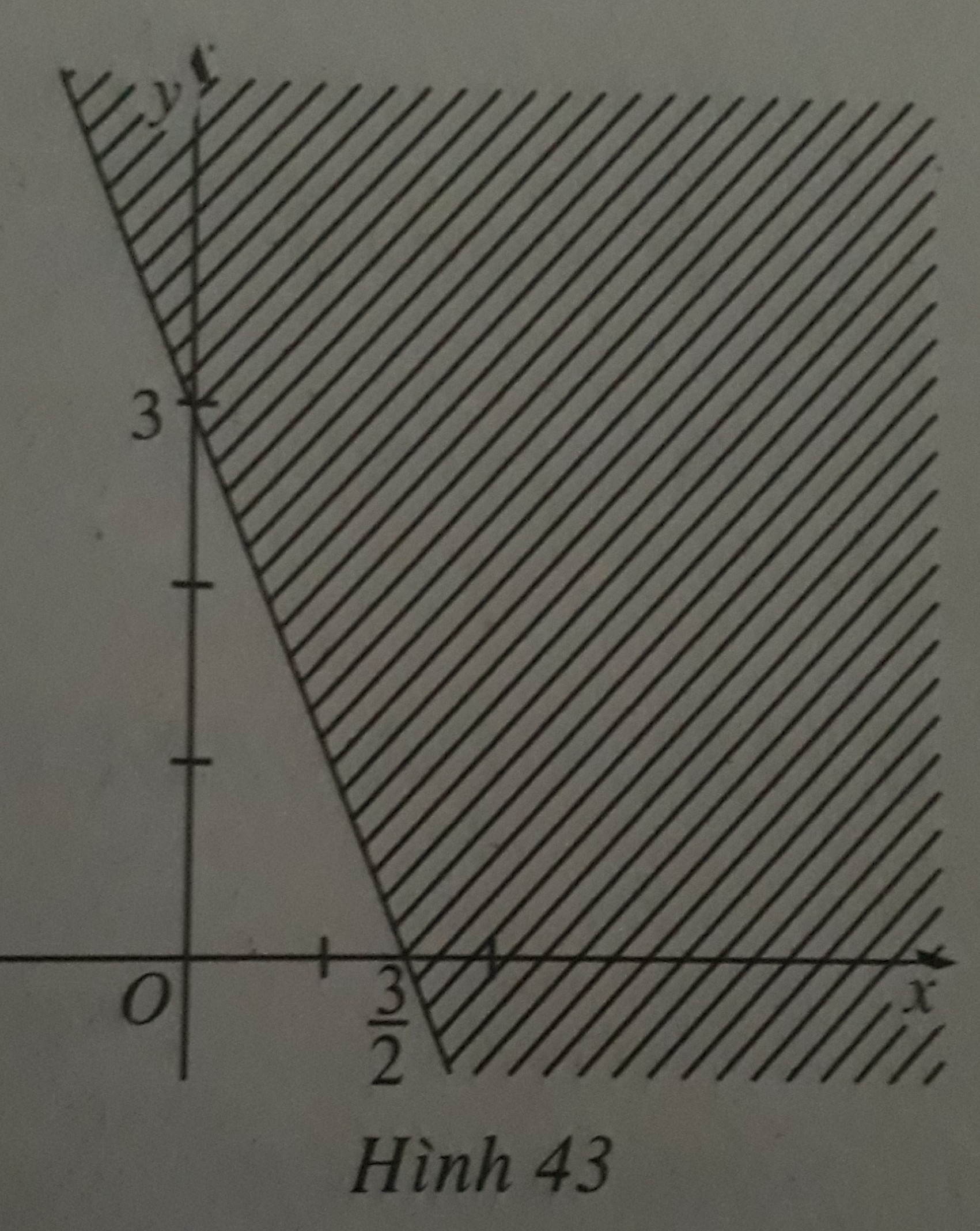
Hình 43 (miền không bị gạch, kể cả biên) biểu diễn miền nghiệm của bất phương trình nào sau đây?

A. x + 2y > 3

B. 2x + y ≤ 3

C. 2x + y < 3

D. x + y - 3 ≤ 0

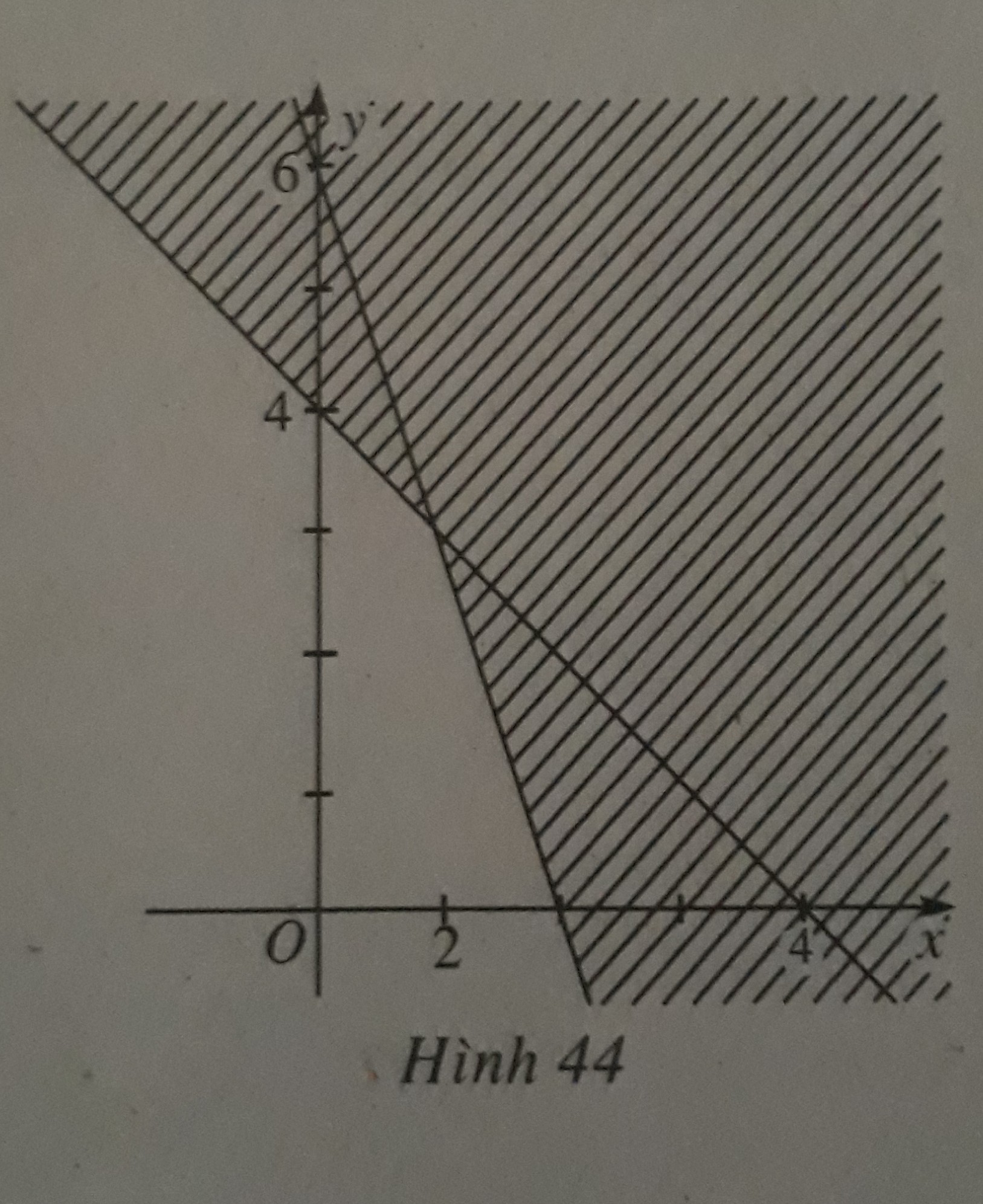
Hình 44 (miền không bị gạch, kể cả biên) biểu diễn miền nghiệm của bất phương trình nào sau đây?

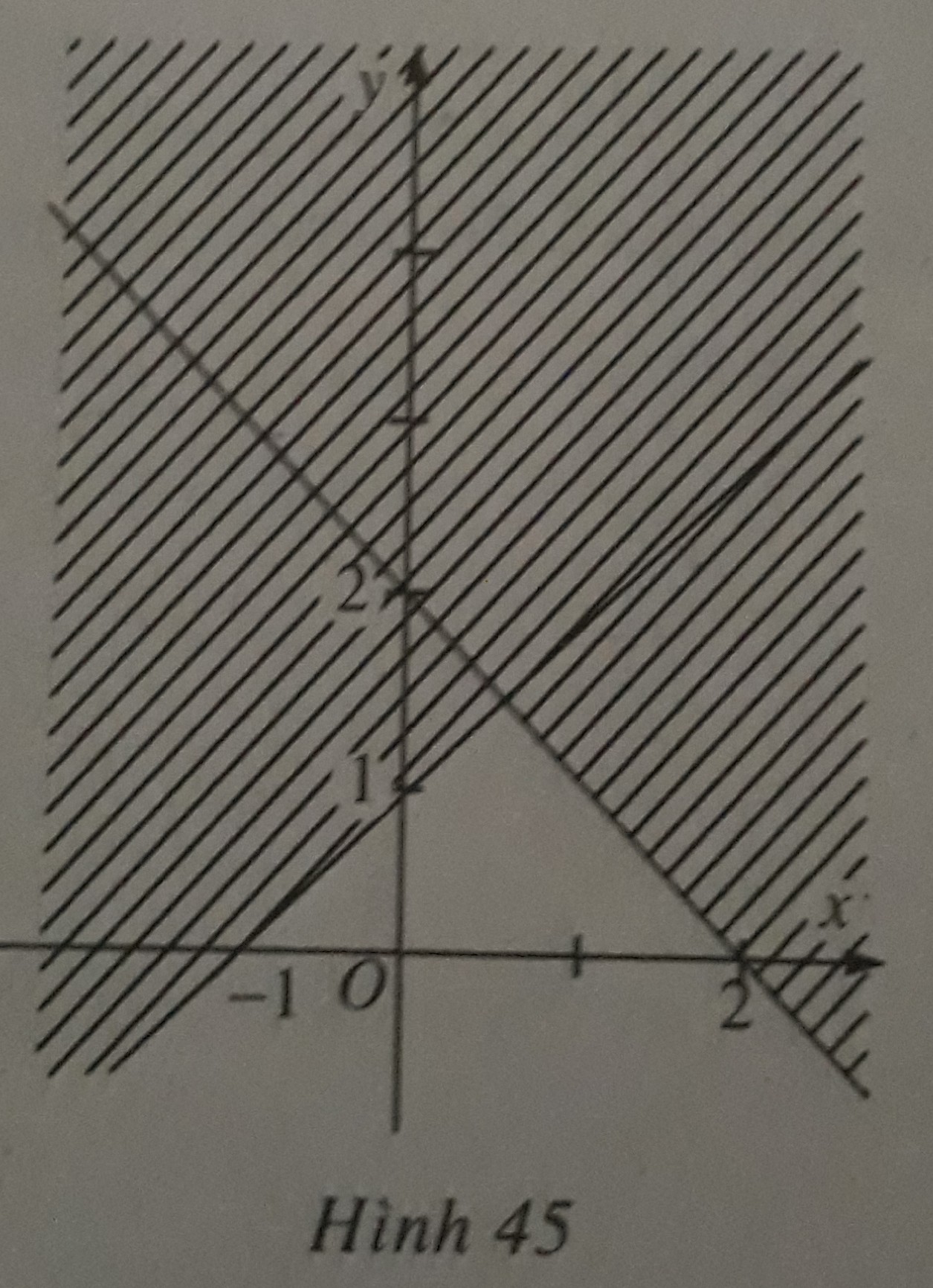
Trong các khẳng định sau, khẳng định nào đúng?

A. Hình 45 (miền không bị gạch, kể cả biên) biểu diễn miền nghiệm của bất phương trình x + y ≤ 2.

B. Hình 45 (miền không bị gạch, kể cả biên) biểu diễn miền nghiệm của bất phương trình \(\left\{ \begin{array}{l}
x + y \le 2\\
x - y + 1 \le 0
\end{array} \right.\) và (x; y) = (-1; 1) là một nghiệm của hệ.

C. Hình 45 (miền không bị gạch, kể cả biên) biểu diễn miền nghiệm của bất phương trình \(\left\{ \begin{array}{l}
x + y \le 2\\
x - y + 1 \ge 0
\end{array} \right.\) và (x; y) = (-2; 1) là một nghiệm của hệ.

D. Hình 45 (miền không bị gạch, kể cả biên) biểu diễn miền nghiệm của bất phương trình \(\left\{ \begin{array}{l}
x + y \le 2\\
x - y + 1 \ge 0
\end{array} \right.\) và (x; y) = (1; 0) là một nghiệm của hệ.

Xác định miền nghiệm của mỗi bất phương trình hai ẩn

a) \(x - 2 + 2\left( {y - 1} \right) > 2x + 4\)

b) \(2x - \sqrt 2 y + \sqrt 2  - 2 \le 0\)

Xác định tập nghiệm của mỗi hệ bất phương trình hai ẩn

a) \(\left\{ \begin{array}{l}
\frac{x}{2} + \frac{y}{3} - 1 > 0\\
2\left( {x - 1} \right) + \frac{y}{2} < 4
\end{array} \right.\)

b) \(\left\{ \begin{array}{l}
4x - 5y + 20 > 0\\
y > 0\\
 - y + 5 > \frac{{x - 3}}{3}
\end{array} \right.\)

Một gia đình cần ít nhất 900 đơn vị protein và 400 đơn vị lipit trong thức ăn mỗi ngày. Mỗi kilôgam thịt bò chứa 800 đơn vị protein và 200 đơn vị lipit. Mỗi kilogam thịt lợn (heo) chứa 600 đơn vị protein và 400 đơn vị lipit. Biết rằng khi gia đình này chỉ mua nhiều nhất là 1,6 kg thịt bò, 1,1 kg thịt lợn, giá tiền 1 kg thịt bò là 45000đ, 1kg thịt lợn lầ 35000đ. Giả sử gia đình mua x kg thịt bò và y kg thịt lợn.

a) Viết các phương trình biểu thị các điều kiện của bài toán thành một hệ bất phương trình rồi xác định miền nghiệm (S) của hệ đó.

b) Gọi T (nghìn đồng) là số tiền phải trả cho x (kilogam) thịt bò và y (kilogam) thịt lợn. Hãy biểu diễn T theo x, y

c) Ở câu a) ta thấy (S) là một miền đa giác. Biết rằng T có giá trị nhỏ nhất tại (x₀;y₀) với (x₀;y0) là tọa độ của một trong các đỉnh của (S). Hỏi gia đình đó phải mua bao nhiêu kilogam thịt mỗi loại để chi phí ít nhất.

Xác định miền nghiệm của các hệ bất phương trình hai ẩn

a) \(x + 3 + 2\left( {2y + 5} \right) < 2\left( {1 - x} \right)\)

b) \(\left( {1 + \sqrt 3 } \right)x - \left( {1 - \sqrt 3 } \right)y \ge 2\)

Xác định miền nghiệm của các hệ bất phương trình hai ẩn

a) \(\left\{ \begin{array}{l}
x - y > 0\\
x - 3y \le  - 3\\
x + y > 5
\end{array} \right.\)

b) \(\left\{ \begin{array}{l}
3x - 2y - 6 \ge 0\\
2\left( {x - 1} \right) + \frac{{3y}}{2} \le 4\\
x \ge 0
\end{array} \right.\)

Gọi (S) là tập hợp các điểm trong mặt phẳng tọa độ có tọa độ thỏa mãn hệ:

\(\left\{ \begin{array}{l}
2x - y \ge 2\\
x - 2y \le 2\\
x + y \le 5\\
x \ge 0
\end{array} \right.\)

a) Hãy xác định (S) để thấy rằng đó là một tam giác.

b) Trong (S) hãy tìm điểm có tọa độ (x;y) làm cho biểu thức f(x;y) = y − x có giá trị nhỏ nhất, biết rằng f(x;y) có giá trị nhỏ nhất tại một trong các đỉnh của (S).

Một nhà khoa học nghiên cứ về tác động phối hợp của vitamin A và vitamin B đối với cơ thể con người. kết quả như sau:

i) Một người có thể tiếp nhận được mỗi ngày không quá 600 đơn vị vitamin A và không quá 500 đơn vị vitamin B.

ii) Một người mỗi ngày cần từ 400 đến 1000 đơn vị vitamin cả A lẫn B.

iii) Do tác động phối hợp của hai loại vitamin A nhưng không nhiều hơn ba lần số đơn vị vitamin A.

Giả sử x và y lần lượt là số đơn vị vitamin A và B mà bạn dùng mỗi ngày

a) Gọi c là số tiền vitamin mà bạn phải trả (tính bằng đồng). hãy viết phương trình biểu diễn c dưới dạng một biểu thức của x và y, nếu giá một đơn vị vitamin A là 9 đồng và giá một đơn vị vitamin B là 7,5 đồng.

b) Viết các phương trình biểu thị i), ii) và iii) , lập thành một hệ bất phương trình rồi biểu diễn miền nghiệm của một hệ bất phương trình đó.

c) Cũng trên mặt phẳng tọa độ ấy, hãy vẽ đường biểu diễn số tiền phải trả c, nếu c =9000, c = 4500; c = 2250

Hãy dùng bút màu để phân biệt các đường đó

d) Tìm phương tán dùng hai loại virtamin A và B thỏa mãn các điều kiện trên để số tiền phải trả là ít nhất.