Bài tập 46 trang 135 SGK Toán 10 NC
Xác định miền nghiệm của các hệ bất phương trình hai ẩn
a) \(\left\{ \begin{array}{l}
x - y > 0\\
x - 3y \le - 3\\
x + y > 5
\end{array} \right.\)
b) \(\left\{ \begin{array}{l}
3x - 2y - 6 \ge 0\\
2\left( {x - 1} \right) + \frac{{3y}}{2} \le 4\\
x \ge 0
\end{array} \right.\)
Hướng dẫn giải chi tiết
a) Ta có \(\left\{ \begin{array}{l}
x - y > 0\\
x - 3y \le - 3\\
x + y > 5
\end{array} \right. \)
\(\Leftrightarrow \left\{ \begin{array}{l}
x - y > 0\\
x - 3y + 3 \le 0\\
x + y - 5 > 0
\end{array} \right.\)
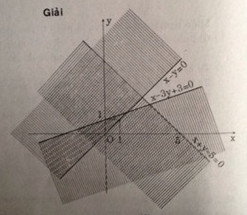
Miền nghiệm là phần mặt phẳng không bị gạch chéo trong đó kể cả những điểm thuộc (d2) và không kể các điểm trên (d1 )và (d3)
Trong đó, (d1): x - y = 0
(d2): x - 3y + 3 = 0
(d3): x + y - 5 = 0
b) Ta có
\(\begin{array}{l}
\left\{ {\begin{array}{*{20}{l}}
{3x - 2y - 6 \ge 0}\\
{2\left( {x - 1} \right) + \frac{{3y}}{2} \le 4}\\
{x \ge 0}
\end{array}} \right.\\
\Leftrightarrow \left\{ {\begin{array}{*{20}{l}}
{3x - 2y - 6 \ge 0}\\
{4x + 3y - 12 \le 0}\\
{x \ge 0}
\end{array}} \right.
\end{array}\)
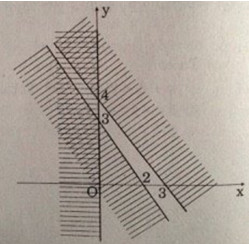
Miền nghiệm là phần mặt phẳng không bị gạch chéo trong đó kể cả những điểm thuộc 3 đường thẳng (d1), (d2), (d3).
Trong đó (d1): 3x - 2y - 6 = 0
(d2): 4x + 3y - 12 = 0
(d3): x = 0
-- Mod Toán 10 HỌC247
Bài tập SGK khác
-


Một bác nông dân cần trồng lúa và khoai trên diện tích đất gồm 6 ha, với lượng phân bón dự trữ là 100kg và sử dụng tối đa 120 ngày công
bởi Nguyễn Sơn Ca
 08/02/2017
08/02/2017
Một bác nông dân cần trồng lúa và khoai trên diện tích đất gồm 6 ha, với lượng phân bón dự trữ là 100kg và sử dụng tối đa 120 ngày công. Để trồng 1 ha lúa cần sử dụng 20kg phân bón, 10 ngày công với lợi nhuận là 30 triệu đồng; để trồng 1 ha khoai cần sử dụng 10kg phân bón, 30 ngày công với lợi nhuận là 60 triệu đồng. Hỏi bác nông dân cần trồng bao nhiêu ha lúa và khoai để đạt lợi nhuận cao nhất.
Theo dõi (0) 1 Trả lời -


Hãy tìm số lượng mỗi loại bánh cần sản xuất sao cho không bị động về nguyên liệu mà lãi đạt được cao nhất.
bởi Nguyễn Thị Thúy
 08/02/2017
08/02/2017
Một cơ sở sản xuất bánh trung thu cần sản xuất 2 loại bánh: bánh thập cẩm và bánh đậu xanh. Lượng đường, đậu cho một bánh mỗi loại, lượng dữ trữ nguyên liệu, tiền lãi cho một bánh mỗi loại được cho trong bảng sau:

Hãy tìm số lượng mỗi loại bánh cần sản xuất sao cho không bị động về nguyên liệu mà lãi đạt được cao nhất.
Theo dõi (0) 1 Trả lời





