Giải bài 3 tr 7 sách GK Toán Hình lớp 10
Cho tứ giác ABCD. Chứng minh rằng tứ giác đó là hình bình hành khi và chỉ khi \(\overrightarrow{AB}=\overrightarrow{DC}\).
Hướng dẫn giải chi tiết bài 3
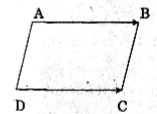
Giả sử tứ giác ABCD là hình bình hành.
Khi đó \(AB = DC \Rightarrow \left| {\overrightarrow {AB} } \right| = \left| {\overrightarrow {DC} } \right|.\)
Mặt khác, dễ thấy \(\overrightarrow {AB} \) và \(\overrightarrow {DC} \) cùng hướng.
Từ đấy, suy ra \(\overrightarrow {AB} = \overrightarrow {DC} \)
Ngược lại, giả sử tứ giác ABCD có \(\overrightarrow {AB} = \overrightarrow {DC} \), đều này chứng tỏ:
\(\overrightarrow {AB} = \overrightarrow {DC} \)và AB // CD
Hay AB = CD và AB // CD
Nên tứ giác ABCD là hình bình hành (dấu hiệu nhận biết hình bình hành).
-- Mod Toán 10 HỌC247
Bài tập SGK khác
Bài tập 1 trang 7 SGK Hình học 10
Bài tập 2 trang 7 SGK Hình học 10
Bài tập 4 trang 7 SGK Hình học 10
Bài tập 1.1 trang 10 SBT Hình học 10
Bài tập 1.2 trang 10 SBT Hình học 10
Bài tập 1.3 trang 10 SBT Hình học 10
Bài tập 1.4 trang 10 SBT Hình học 10
Bài tập 1.5 trang 10 SBT Hình học 10
Bài tập 1.6 trang 10 SBT Hình học 10
Bài tập 1.7 trang 10 SBT Hình học 10
Bài tập 1 trang 8 SGK Hình học 10 NC
Bài tập 2 trang 8 SGK Hình học 10 NC
Bài tập 3 trang 8 SGK Hình học 10 NC
-


Gọi O là tâm hình lục giác đều ABCDEF. Hãy chỉ ra các vectơ bằng \(\overrightarrow {OA} \)
bởi hồng trang
 20/02/2021
Theo dõi (0) 1 Trả lời
20/02/2021
Theo dõi (0) 1 Trả lời -


Khẳng định sau đúng hay sai: Nếu ba điểm phân biệt A, B, C thẳng hàng thì hai vectơ \(\overrightarrow {AB} \) và \(\overrightarrow {BC} \) cùng hướng.
bởi Ho Ngoc Ha
 19/02/2021
Theo dõi (0) 1 Trả lời
19/02/2021
Theo dõi (0) 1 Trả lời -


Hãy nhận xét về vị trí tương đối của các giá của các cặp vectơ sau: \(\overrightarrow {AB} \) và \(\overrightarrow {CD} \), \(\overrightarrow {PQ} \) và \(\overrightarrow {RS} \), \(\overrightarrow {EF} \) và \(\overrightarrow {PQ} \).
bởi Ho Ngoc Ha
 19/02/2021
19/02/2021
.png) Theo dõi (0) 1 Trả lời
Theo dõi (0) 1 Trả lời





