Giải bài 1.4 tr 10 SBT Hình học 10
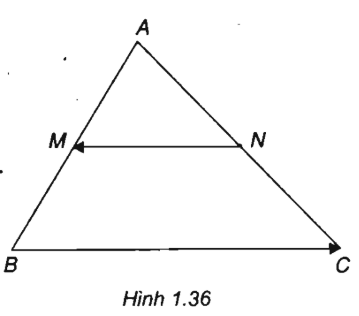
Cho tam giác ABC. Các điểm M và N lần lượt là trung điểm của các cạnh AB và AC. So sánh độ dài của hai vec tơ \(\overrightarrow {NM} \), \(\overrightarrow {BC} \). Vì sao có thể nói hai vec tơ này cùng phương?
Hướng dẫn giải chi tiết
Vì MN là đường trung bình của ΔABC nên MN//BC và \(MN = \frac{1}{2}BC\), hay \(\left| {\overrightarrow {MN} } \right| = \frac{1}{2}\left| {\overrightarrow {BC} } \right|\).
Vì MN//BC nên \(\overrightarrow {NM} \) và \(\overrightarrow {BC} \) cùng phương.
-- Mod Toán 10 HỌC247
Bài tập SGK khác
Bài tập 1.2 trang 10 SBT Hình học 10
Bài tập 1.3 trang 10 SBT Hình học 10
Bài tập 1.5 trang 10 SBT Hình học 10
Bài tập 1.6 trang 10 SBT Hình học 10
Bài tập 1.7 trang 10 SBT Hình học 10
Bài tập 1 trang 8 SGK Hình học 10 NC
Bài tập 2 trang 8 SGK Hình học 10 NC
Bài tập 3 trang 8 SGK Hình học 10 NC
-
cho ngũ giác ABCDE có bao nhiêu vecto khác 0 có điểm đầu cuối là đỉnh của ngũ giác đã cho?
Theo dõi (0) 2 Trả lời -
Bài 1.7 trang 12 sách bài tập Toán 10
bởi Vũ Hải Yến
02/10/2018
Bài 1.7 (STB trang 12)Cho hình bình hành ABCD. Dựng \(\overrightarrow{AM}=\overrightarrow{BA};\overrightarrow{MN}=\overrightarrow{DA};\overrightarrow{NP}=\overrightarrow{DC};\overrightarrow{PQ}=\overrightarrow{BC}\). Chứng minh \(\overrightarrow{AQ}=\overrightarrow{0}\) ?
Theo dõi (0) 1 Trả lời -
Bài 1.6 trang 12 sách bài tập Toán 10
bởi Ngoc Nga
02/10/2018
Bài 1.6 (STB trang 12)Xác định vị trí tương đối của ba điểm phân biệt A, B và C trong các trường hợp sau :
a) \(\overrightarrow{AB}\) và \(\overrightarrow{AC}\) cùng hướng, \(\left|\overrightarrow{AB}\right|>\left|\overrightarrow{AC}\right|\)
b) \(\overrightarrow{AB}\) và \(\overrightarrow{AC}\) ngược hướng
c) \(\overrightarrow{AB}\) và \(\overrightarrow{AC}\) cùng phương
Theo dõi (0) 1 Trả lời
