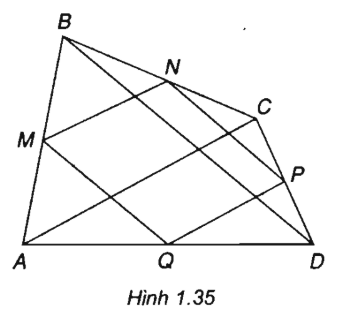
Bài tập 1.3 trang 10 SBT Hình học 10

Ta thấy, MN là đường trung bình của tam giác ABC nên MN//AC và \[MN = \frac{1}{2}AC\)

PQ là đường trung bình của tam giác ADC nên PQ//AC và \[PQ = \frac{1}{2}AC\).

Do đó NM//PQ và MN = PQ.

Vậy tứ giác MNPQ là hình bình hành nên \(\overrightarrow {NP}  = \overrightarrow {MQ} \) và \(\overrightarrow {PQ}  = \overrightarrow {NM} \)

-- Mod Toán 10 HỌC247