Toán 10 Cánh Diều Bài 6: Ba đường conic

Vi dụ: Cho elip có phương trình chính tắc \(\frac{{{x^2}}}{{25}} + \frac{{{y^2}}}{{16}} = 1\). Tìm các tiêu điểm và tiêu cự của elip. Tính tổng các khoảng cách từ mỗi điểm trên elip tới hai tiêu điểm.

Giải

Ta có: a2 = 25, b2 = 16. Do đó \(c = \sqrt {{a^2} - {b^2}}  = 3\). Vậy elip có hai tiêu điểm là \({F_1}\left( { - 3;0} \right);{F_2}\left( {3;0} \right)\) và tiêu cự là \({F_1}{F_2} = 2c = 6\). Ta có \(a = \sqrt {25}  = 5\), nên tổng các khoảng cách từ mỗi điểm trên elip tới hai tiêu điểm bằng 2a= 10. 

Cho hai điểm phân biệt có định \({F_1}\) và \({F_2}\). Đặt \({F_1}{F_2} = 2c\). Cho số thực dương a nhỏ hơn c. Tập hợp các điểm M sao cho \(\left| {M{F_1} - M{F_2}} \right| = 2c\) được gọi là đường hypebol (hay hypebol). Hai điểm \({{F_1},{F_2}}\) được gọi là hai tiêu điểm và \({F_1}{F_2} = 2c\) được gọi là tiêu cự của hypebol đó.

Ví dụ: Cho hypebol có phương trình chính tắc \(\frac{{{x^2}}}{9} - \frac{{{y^2}}}{{16}} = 1\). Tìm các tiêu điểm và tiêu cự của hypebol. Hiệu các khoảng cách từ một điểm nằm trên hypebol tới hai tiêu điểm có giá trị tuyệt đối bằng bao nhiêu?

Giải

Ta có \({a^2} = 9,{b^2} = 16\), nên \(c = \sqrt {{a^2} + {b^2}}  = 5\). Vậy hypebol có hai tiêu điểm là \({F_1}\left( { - 5;0} \right),{F_2}\left( {5;0} \right)\) và có tiêu cự 2c = 10. Hiệu các khoảng cách từ một điểm nằm trên hypebol tới hai tiêu điểm có giá trị tuyệt đối bằng \(2{\rm{a}} = 2\sqrt 9  = 6\). 

Ví dụ: Cho parabol \((P):{y^2} = x\). 

a) Tìm tiêu điểm F, đường chuẩn \(\Delta \) của (P).

b) Tìm những điểm trên (P) có khoảng cách tới F bằng 3. 

Giải

a) Ta có 2p = 1 nên \(p = \frac{1}{2}\). 

Parabol có tiêu điểm \(F\left( {\frac{1}{4};0} \right)\) và đường chuẩn \(\Delta :x =  - \frac{1}{4}\) 

b) Điểm \(M\left( {{x_0};{y_0}} \right)\) thuuọc (P) có khoảng các tới F bằng 3 khi và chỉ khi \({y_0}^2 = {x_0}\) và MF = 3.

Do \(MF = d\left( {M,\Delta } \right)\) nên \(d\left( {M,\Delta } \right) = 3\)

Mặt khác \(\Delta :x + \frac{1}{4} = 0\) và \({x_0} = {y_0}^2 \ge 0\) nên \(3 = d\left( {M,\Delta } \right) = \left| {{x_0} + \frac{1}{4}} \right| = {x_0} + \frac{1}{4}.\)

Vậy \({x_0} = \frac{{11}}{4}\) và \({y_0} = \frac{{\sqrt {11} }}{2}\) hoặc \({y_0} =  - \frac{{\sqrt {11} }}{2}\). 

Vậy có hai điểm M thoả mãn bài toán với toạ độ là \(\left( {\frac{{11}}{4};\frac{{\sqrt {11} }}{2}} \right)\) và \(\left( {\frac{{11}}{4}; - \frac{{\sqrt {11} }}{2}} \right)\).  

- Ba đường conic có nhiều ứng dụng trong thực tiễn. Ta nêu ra một vài ứng dụng của ba đường conic.

+ Năm 1911, nhà vật lí học người Anh là Ernest Rutherford (1871 - 1937) đã để xuất mô hình hành tỉnh nguyên tử, trong đó hạt nhân nhỏ bé nằm tại tâm của nguyên tử, còn các electron bay quanh hạt nhân trên các quỹ đạo hình elip như các hành tỉnh bay quanh Mặt Trời (Hình sau).

+ Trong vật lí, hiện tượng hai sóng gặp nhau tạo nên các gợn sóng ổn định gọi là hiện tượng giao thoa của hai sóng. Các gợn sóng có hình các đường hypebol gọi là các vân giao thoa (Hình sau).

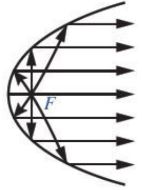
+ Với gương parabol, tia sáng phát ra từ tiêu điểm (tia tới) chiếu đến một điểm của parabol sẽ bị hắt lại (ủa phản xạ) theo một tỉa song song (hoặc trùng) với trục của parabol (Hình sau).

- Tính chất trên có nhiều ứng dụng, chẳng hạn:

+ Đèn pha: Bề mặt của đèn pha là một mặt tròn xoay sinh bởi một cung parabol quay quanh trục của nó, bóng đèn được đặt ở vị trí tiêu điểm của parabol đó (Hình sau). Các tia sáng phát ra từ bóng đèn khi chiếu đến bề mặt của đèn pha sẽ bị hắt lại theo các tỉa sáng song song, cho phép chúng ta quan sát được các vật ở xa.

+ Chảo vệ tỉnh cũng có dạng như đèn pha. Điểm thu và phát tín hiệu của máy được đặt ở vị trí tiêu điểm của parabol (Hình sau).

Câu 1: Lập phương trình chính tắc của elip (E) đi qua hai điểm M(0 ; 3) và \(N\left( {3; - \frac{{12}}{5}} \right)\)

Hướng dẫn giải

Elip có phương trình chính tắc là: \(\frac{{{x^2}}}{{{a^2}}} + \frac{{{y^2}}}{{{b^2}}} = 1\left( {a > b > 0} \right)\)

Do Elip đi qua điểm M(0;3) nên \(b = 3\)

Điểm \(N\left( {3; - \frac{{12}}{5}} \right)\) thuộc (E) nên ta có: \(\frac{{{3^2}}}{{{a^2}}} + \frac{{{{\left( { - \frac{{12}}{5}} \right)}^2}}}{{{3^2}}} = 1 \Leftrightarrow a = 5\)

Vậy Elip có phương trình chính tắc là: \(\frac{{{x^2}}}{{25}} + \frac{{{y^2}}}{9} = 1\)

Câu 2: Viết phương trình hypebol sau đây dưới dạng chính tắc: \(4{x^2}-9{y^2} = {\rm{ }}1.\)

Hướng dẫn giải

Ta có: \(4{x^2}-9{y^2} = {\rm{ }}1 \Leftrightarrow \frac{{{x^2}}}{{{{\left( {\frac{1}{4}} \right)}^2}}} - \frac{{{y^2}}}{{{{\left( {\frac{1}{9}} \right)}^2}}} = 1\)

Vậy phương trình chính tắc của hypebol là: \(\frac{{{x^2}}}{{{{\left( {\frac{1}{4}} \right)}^2}}} - \frac{{{y^2}}}{{{{\left( {\frac{1}{9}} \right)}^2}}} = 1\) 

Câu 3: Viết phương trình các parabol sau đây dưới dạng chính tắc:

a) \(x = \frac{{{y^2}}}{4}\)

b) \(x-y^2=0\) 

Hướng dẫn giải 

a) \(x = \frac{{{y^2}}}{4} \Leftrightarrow {y^2} = 4x\)

Vậy dạng chính tắc của parabol là: \({y^2} = 4x\)

b) \(x - {y^2} = 0 \Leftrightarrow {y^2} = x\)

Vậy dạng chính tắc của parabol là: \({y^2} = x\) 

Qua bài giảng trên, giúp các em học sinh:

- Nắm vững được khái niệm và phương trình đường chuẩn của (E) và (H).

- Nắm vững được định nghĩa ba đường conic.

- Xác định được phương trình đường chuẩn của các đường conic.

- Lập được phương trình của cônic khi biết phương trình đường chuẩn và tâm sai của nó.

Để củng cố bài học xin mời các em cùng làm Bài kiểm tra Trắc nghiệm Toán 10 Cánh Diều Chương 7 Bài 6 để kiểm tra xem mình đã nắm được nội dung bài học hay chưa.

• Câu 1:

  Cho elip (E) có phương trình \(\frac{{{x^2}}}{{36}}\; + \;\frac{{{y^2}}}{{16}}\; = \;1\). Đường thẳng nào sau đây cắt (E) tại hai điểm đối xứng nhau qua trục Oy?

  • A. y = 2x 
  • B. y = 3 
  • C. x = 3 
  • D. y = 10 

• Câu 2:

  Phương trình chính tắc của elip có độ dài trục nhỏ bằng 8, hình chữ nhật cơ sở có chu vi bằng 40 là:

  • A. \(\frac{{{x^2}}}{{36}}\; + \;\frac{{{y^2}}}{{16}}\; = \;1\) 
  • B. \(36{x^2}\; + \;16{y^2}\; = \;1\) 
  • C. \(\frac{{{x^2}}}{{144}}\; + \;\frac{{{y^2}}}{{64}}\; = \;1\) 
  • D. \(36{x^2}\; + \;16{y^2}\; = \;576\) 

• Câu 3:

  Phương trình nào sau đây là phương trình chính tắc của một elip?

  • A. \(\frac{{{x^2}}}{9}\; + \;\frac{{{y^2}}}{{16}}\; = \;1\) 
  • B. \(\frac{{{x^2}}}{{12}}\; + \;\frac{{{y^2}}}{{12}}\; = \;1\) 
  • C. \(\frac{{{x^2}}}{{16}}\; + \;\frac{{{y^2}}}{4}\; = \;1\) 
  • D. \(12{x^2}\; + \;3{y^2}\; = \;1\) 

Câu 4-10: Mời các em đăng nhập xem tiếp nội dung và thi thử Online để củng cố kiến thức và nắm vững hơn về bài học này nhé!

Bên cạnh đó các em có thể xem phần hướng dẫn Giải bài tập Toán 10 Cánh Diều Chương 7 Bài 6 để giúp các em nắm vững bài học và các phương pháp giải bài tập.

Hoạt động 1 trang 93 SGK Toán 10 Cánh diều tập 2 - CD

Hoạt động 2 trang 94 SGK Toán 10 Cánh diều tập 2 - CD

Luyện tập 1 trang 95 SGK Toán 10 Cánh diều tập 2 - CD

Hoạt động 3 trang 96 SGK Toán 10 Cánh diều tập 2 - CD

Hoạt động 4 trang 97 SGK Toán 10 Cánh diều tập 2 - CD

Luyện tập 2 trang 98 SGK Toán 10 Cánh diều tập 2 - CD

Hoạt động 5 trang 99 SGK Toán 10 Cánh diều tập 2 - CD

Luyện tập 3 trang 100 SGK Toán 10 Cánh diều tập 2 - CD

Giải bài 1 trang 102 SGK Toán 10 Cánh diều tập 2 - CD

Giải bài 2 trang 102 SGK Toán 10 Cánh diều tập 2 - CD

Giải bài 3 trang 102 SGK Toán 10 Cánh diều tập 2 - CD

Giải bài 4 trang 102 SGK Toán 10 Cánh diều tập 2 - CD

Giải bài 5 trang 102 SGK Toán 10 Cánh diều tập 2 - CD

Giải bài 6 trang 102 SGK Toán 10 Cánh diều tập 2 - CD

Giải bài 7 trang 102 SGK Toán 10 Cánh diều tập 2 - CD

Giải bài 8 trang 102 SGK Toán 10 Cánh diều tập 2 - CD

Giải bài 9 trang 102 SGK Toán 10 Cánh diều tập 2 - CD

Giải bài 10 trang 102 SGK Toán 10 Cánh diều tập 2 - CD

Giải bài 11 trang 102 SGK Toán 10 Cánh diều tập 2 - CD

Giải bài 59 trang 95 SBT Toán 10 Cánh diều tập 2 - CD

Giải bài 60 trang 95 SBT Toán 10 Cánh diều tập 2 - CD

Giải bài 61 trang 96 SBT Toán 10 Cánh diều tập 2 - CD

Giải bài 62 trang 96 SBT Toán 10 Cánh diều tập 2 - CD

Giải bài 63 trang 96 SBT Toán 10 Cánh diều tập 2 - CD

Giải bài 64 trang 97 SBT Toán 10 Cánh diều tập 2 - CD

Giải bài 65 trang 97 SBT Toán 10 Cánh diều tập 2 - CD

Giải bài 66 trang 97 SBT Toán 10 Cánh diều tập 2 - CD

Giải bài 67 trang 97 SBT Toán 10 Cánh diều tập 2 - CD

Giải bài 68 trang 97 SBT Toán 10 Cánh diều tập 2 - CD

Giải bài 69 trang 97 SBT Toán 10 Cánh diều tập 2 - CD

Giải bài 70 trang 97 SBT Toán 10 Cánh diều tập 2 - CD

Trong quá trình học tập nếu có thắc mắc hay cần trợ giúp gì thì các em hãy comment ở mục Hỏi đáp, Cộng đồng Toán HOC247 sẽ hỗ trợ cho các em một cách nhanh chóng!

Chúc các em học tập tốt và luôn đạt thành tích cao trong học tập!