-
Câu hỏi:
Cho tam giác ABC nhọn. Đường tròn đường kính BC cắt AB tại N, AC tại M. Gọi H là giao điểm của CN và BM. Khi đó A,N,H,M cùng nằm trên đường tròn nào?
-
A.
\((I;IM)\), I là trung điểm MN
-
B.
\((I;IH)\), I là trung điểm MN
-
C.
\((F;FA)\), F là giao điểm đường tròn với AH
-
D.
\((E;EA)\), E là trung điểm AH
Lời giải tham khảo:
Đáp án đúng: D
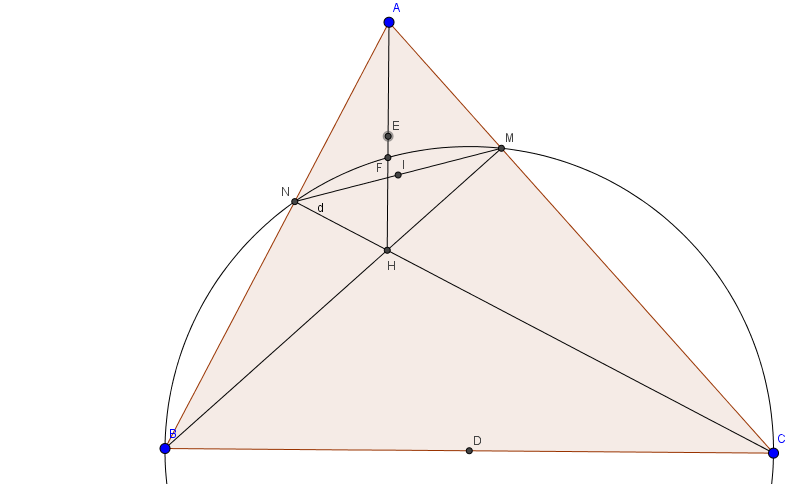
Trước tiên: hai tam giác BNC và BMC là hai tam giác lần lượt vuông tại N và M. Đường tròn đường kính BC đi qua M,N
Xét hai tam giác ANH và AMH cũng lần lượt vuông tại N,M. Với E là trung điểm AH, Ah là cnahj huyền của cả hai tam giác
nên đường tròn tâm E bán kính EA sẽ đi qua M, N, H.
Hãy trả lời câu hỏi trước khi xem đáp án và lời giải -
A.
Câu hỏi này thuộc đề thi trắc nghiệm dưới đây, bấm vào Bắt đầu thi để làm toàn bài
CÂU HỎI KHÁC
- Cho hai đường thẳng xy và xy cuông góc với nhau cắt nhau tại O.Một đoạn thẳng AB=8 chuyển động sao cho A luôn nằm trên xy và B luôn nằm x'y'
- Cho hình thang ABCD (ABparallel CD), widehat{C}=widehat{D}=60^{circ}, CD=2AD=8. Khi đó A, B, C, D luôn thuộc đường tròn nào?
- Cho tam giác ABC có BH, CE là các đường cao. Gọi M là giao điểm BH và CE. I là trung điểm BC. Khi đó B,C,E,H cùng thuộc đường tròn nào?
- Cho đường tròn tâm A đường kính BC. Gọi D là trung điểm AB. Dây EF vuông góc với AB tại D. Tứ giác EBFA là hình gì?
- Cho tam giác ABC nhọn. Đường tròn đường kính BC cắt AB tại N, AC tại M. Gọi H là giao điểm của CN và BM. Khi đó A,N,H,M cùng nằm trên đường tròn nào?


