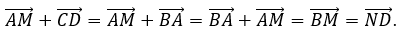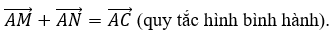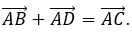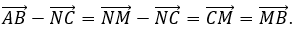-
Câu hỏi:
Cho hình bình hành ABCD. Hai điểm M và N lần lượt là trung điểm của BC và AD. Cặp vectơ nào trong số các cặp vectơ sau đây không bằng nhau?
-
A.
\(\overrightarrow {NC} + \overrightarrow {MC} \) và \(\overrightarrow {AD} \)
-
B.
\(\overrightarrow {AM} + \overrightarrow {CD} \) và \(\overrightarrow {ND} \)
-
C.
\(\overrightarrow {AB} - \overrightarrow {NC} \) và \(\overrightarrow {MB} \)
-
D.
\(\overrightarrow {AM} + \overrightarrow {AN} \) và \(\overrightarrow {AB} + \overrightarrow {AD} \)
Lời giải tham khảo:
Đáp án đúng: A
Vì \(\overrightarrow {MC} = \overrightarrow {AN} \)
Ta có \(\overrightarrow {NC} + \overrightarrow {MC} = \overrightarrow {NC} + \overrightarrow {AN} = \overrightarrow {AN} + \overrightarrow {NC} = \overrightarrow {AC} \ne \overrightarrow {AD} \)
Chọn A.
Lưu ý: Trong phương án B, vì CD→=BA→, ta có
Trong phương án D, vì tứ giác AMCN là hình bình hành nên ta có:
Vì tứ giác ABCD là hình bình hành nên
Suy ra
Trong phương án C,
Chọn A.
Hãy trả lời câu hỏi trước khi xem đáp án và lời giải -
A.
Câu hỏi này thuộc đề thi trắc nghiệm dưới đây, bấm vào Bắt đầu thi để làm toàn bài
CÂU HỎI KHÁC
- Vectơ tổng hợp của hai vectơ như hình vẽ sau có độ lớn là? (giả sử ô vuông có đơn vị là cm)
- Vectơ tổng hợp của hai vectơ trong hình sau có độ lớn là?
- Cho 2 điểm phân biệt A và B. Tập hợp các điểm O thỏa mãn vec{OA}=vec{OB} là:
- Vectơ đối của tổng sau vec{a}+vec{b}-vec{c} là:
- Cho tam giác ABC vuông tại A có \(AB = \sqrt 5 ,AC = 2\sqrt 5 \). Độ dài vectơ AB→ + AC→ bằng:
- Cho hình bình hành ABCD. Hai điểm M và N lần lượt là trung điểm của BC và AD.
- Cho tam giác ABC. Vectơ \(\overrightarrow {AB} + \overrightarrow {AC} \) có giá trị chứa đường thẳng nào sau đây?
- Cho tam giác ABC vuông tại A và AB = 3, AC = 8. Vectơ \(\overrightarrow {CB} + \overrightarrow {AB} \) có độ dài là:
- Cho tam giác ABC. Các điểm M, N và P lần lượt là trung điểm của các cạnh AB, AC và BC.
- Cho tam giác đều ABC cạnh a, đường cao AH. Hỏi a√3 là độ dài của vectơ nào trong số các vectơ sau đây?




.PNG)