-
Câu hỏi:
Cho hàm số \(y=f\left( 2-x \right)\) có BBT như sau:
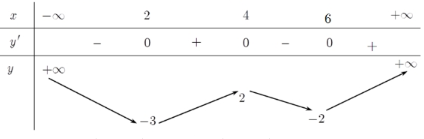
Tổng các giá trị nguyên của tham số \(m\) để phương trình \(3{{f}^{2}}\left( {{x}^{2}}-4x \right)-\left( m+2 \right)f\left( {{x}^{2}}-4x \right)+m-1=0\) có đúng 8 nghiệm thực phân biệt thuộc khoảng \(\left( 0;+\infty \right)\)?
-
A.
7
-
B.
-6
-
C.
3
-
D.
-3
Lời giải tham khảo:
Đáp án đúng: B
Xét hàm số \(g\left( x \right)=f\left( {{x}^{2}}-4x \right)\).
Có \(g'\left( x \right)=\left( 2x-4 \right)f'\left( {{x}^{2}}-4x \right)\). Cho
\(\begin{array}{l}
g'\left( x \right) = 0\\
\Leftrightarrow \left[ \begin{array}{l}
x = 2\\
f'\left( {{x^2} - 4x} \right) = 0\,\,\,\,\left( 1 \right)
\end{array} \right.
\end{array}\).Ta có:
\(\begin{array}{l}
f'\left( {{x^2} - 4x} \right) = 0\\
\Leftrightarrow \left[ \begin{array}{l}
{x^2} - 4x = - 4\\
{x^2} - 4x = - 2\\
{x^2} - 4x = 0
\end{array} \right.\\
\Leftrightarrow \left[ \begin{array}{l}
x = 2\\
x = 2 \pm \sqrt 2 \\
\left[ \begin{array}{l}
x = 0\\
x = 4
\end{array} \right.
\end{array} \right.
\end{array}\)Bảng biến thiên
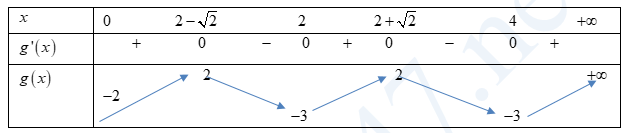
Lại có: \(3{{f}^{2}}\left( {{x}^{2}}-4x \right)-\left( m+2 \right)f\left( {{x}^{2}}-4x \right)+m-1=0\)\(\Leftrightarrow 3{{g}^{2}}\left( x \right)-\left( m+2 \right)g\left( x \right)+m-1=0\,\,\left( 2 \right)\).
Ta có: \(\Delta ={{\left( m+2 \right)}^{2}}-4.3.\left( m-1 \right)0={{m}^{2}}-8m+16={{\left( m-4 \right)}^{2}}>0,\forall m\ne 4\).
Dựa vào bảng biến thiên ta thấy phương trình \(g\left( x \right)=h\left( m \right)\) có tối đa là 5 nghiệm phân biệt
Do đó, để phương trình \(3{{f}^{2}}\left( {{x}^{2}}-4x \right)-\left( m+2 \right)f\left( {{x}^{2}}-4x \right)+m-1=0\) có đúng 8 nghiệm phân biệt thì
TH1. \(\left\{ \begin{array}{l}
g\left( x \right) = 2\\
- 2 < g\left( x \right) < 2
\end{array} \right.\).Thế \(g\left( x \right)=2\) vào phương trình (2) ta được \(m=7\). Khi \(m=7\), phương trình (2) có hai nghiệm
\(\left[ \begin{array}{l}
g\left( x \right) = 2\\
g\left( x \right) = 1
\end{array} \right.\) thỏa yêu cầu.TH2. \(\left\{ \begin{array}{l}
- 3 < g\left( x \right) < - 2\\
- 2 < g\left( x \right) < 2
\end{array} \right.\)\( \Leftrightarrow \left\{ \begin{array}{l}
- 3 < \frac{{m + 2 - \sqrt {{{\left( {m - 4} \right)}^2}} }}{6} < - 2\\
- 2 < \frac{{m + 2 + \sqrt {{{\left( {m - 4} \right)}^2}} }}{6} < 2
\end{array} \right.\)\( \Leftrightarrow \left\{ \begin{array}{l}
- 3 < \frac{{m + 2 - \sqrt {{{\left( {m - 4} \right)}^2}} }}{6} < - 2\\
- 2 < \frac{{m + 2 + \sqrt {{{\left( {m - 4} \right)}^2}} }}{6} < 2
\end{array} \right.\)Với \(m\ge 4\), ta có:
\(\Leftrightarrow \left\{ \begin{array}{l} - 18 < 6 < - 12\\ - 12 < 2m - 2 < 12 \end{array} \right.\)(vô lí).
Với \(m < 4\), ta có:
\(\Leftrightarrow \left\{ \begin{array}{l} - 18 < 2m - 2 < - 12\\ - 12 < 6 < 12 \end{array} \right. \)\( \Leftrightarrow - 8 < m < - 5\).
Vậy có tổng các giá trị nguyên của tham số \(m\) thỏa yêu cầu đề bài là \(7+\left( -7 \right)+\left( -6 \right)=-6\).
Chọn B
Hãy trả lời câu hỏi trước khi xem đáp án và lời giải -
A.
Câu hỏi này thuộc đề thi trắc nghiệm dưới đây, bấm vào Bắt đầu thi để làm toàn bài
CÂU HỎI KHÁC
- Nghiệm của phương trình sau \({{\left( \frac{1}{5} \right)}^{{{x}^{2}}-2x-3}}={{5}^{x+1}}\) là?
- Cho hình chóp tứ giác \(S.ABCD\) có đáy \(ABCD\) là hình vuông cạnh \(2a\), cạnh bên \(SA\) vuông góc
- Cho hàm số \(y=\frac{x+2}{x-1}\). Xét các mệnh đề sau đây: Số các mệnh đề đúng là?
- Tính thể tích của khối chóp có diện tích đáy \(B=6\) và chiều cao \(h=4\) là?
- Cho HS \(y=f\left( x \right)\) liên tục trên \(\mathbb{R}\) có bảng xét dấu của \({f}'\left( x \right)\) như sau: Số điểm cực tiểu của hàm số đã cho là?
- Cho biết thể tích \(V\) của khối trụ có chiều cao \(h=4\) cm và bán kính đáy \(r=3\) cm bằng?
- Gọi \(n\) là số nguyên dương bất kì, \(n\ge 2\), công thức nào đúng?
- Cho hàm số \(y=f\left( x \right)\) có đạo hàm trên \(\mathbb{R}\)và hàm số \(y={f}'\left( x \right)\) là
- Gọi \(l,h,r\) lần lượt là độ dài đường sinh, chiều cao và bán kính mặt đáy. Diện tích xung quanh \({{S}_{xq}}\) của hình nón là?
- Cho biểu thức \(\sqrt[3]{4\sqrt{2\sqrt[5]{8}}}={{2}^{\frac{m}{n}}}\), trong đó \(\frac{m}{n}\) là phân số
- Tìm tất cả các giá trị thực của tham số \(m\) để hàm số sau \(y=\ln \left( {{x}^{2}}-2mx+4 \right)\) có tập xác định là \(\mathbb{R}\)?
- Cho hàm số \(y=f\left( x \right)\) liên tục trên đoạn \(\left[ -1;2 \right]\) và có đồ thị như hình.
- Cho CSN \(\left( {{u}_{n}} \right)\) có \({{u}_{1}}=2\) và công bội \(q=-3\). Giá trị của \({{u}_{2}}\) bằng?
- Hình bát diện đều thuộc loại khối đa diện nào?
- Cho hàm số \(y=\frac{ax+b}{cx-1}\) có đồ thị như hình. Giá trị của tổng \(S=a+b+c\) bằng?
- Tích tất cả các nghiệm của phương trình \(\log _{3}^{2}x-2{{\log }_{3}}x-7=0\) là?
- Cho lăng trụ tam giác \(ABC.A'B'C'\) có thể tích bằng \(V\). Khi đó, thể tích khối chóp \(A.AB{{C}^{'}}\) bằng?
- Đồ thị hàm số nào dưới đây có dạng như đường cong trong hình?
- Với các số \(a,\ b>0\) thỏa mãn \({{a}^{2}}+{{b}^{2}}=7ab\), giá trị biểu thức \({{\log }_{3}}\left( a+b \right)\) bằng?
- Tổng số đường tiệm cận đứng và ngang của ĐTHS \(y=\frac{\sqrt{1-{{x}^{2}}}}{{{x}^{2}}+2x}\) là?
- Gọi \(M,m\) lần lượt là GTLN, GTNN của hàm số \(y={{x}^{3}}-3{{x}^{2}}-9x-1\) trên đoạn\(\left[ 1;5 \right]\). Tính giá trị \(T=2M-m\)?
- Cho ĐTHS \(y=f\left( x \right)\) liên tục trên \(\mathbb{R}\) và có đồ thị như hình: Số nghiệm của phương trình \(\left| 2f\left( x \right)-3 \right|=1\) là?
- TXĐ của hàm số \(y={{\left( 1-x \right)}^{-2}}\) là?
- Hàm số nào bên dưới đây không có cực trị?
- Mệnh đề nào dưới đây sai?
- Cho \(x,y>0\) và \(\alpha ,\beta \in \mathbb{R}\). Tìm đẳng thức sai?
- Tập nghiệm của bất phương trình sau \({{2}^{x\,-\,3}}\,>\,8\) là?
- Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình chữ nhật, \(AB=3,\,AD=4\) và các cạnh bên của hình
- Cho hàm số \(y=f\left( x \right)\) xác định trên tập \(D\). Số \(M\) được gọi là GTLN của hàm số \(y=f\left( x \right)\) trên \(D\) nếu?
- Cho hàm số \(f\left( x \right)\) có BBT như sau: Giá trị cực đại của hàm số đã cho là?
- Có tất cả bao nhiêu giá trị nguyên của tham số \(m\) để hàm số \(f\left( x \right)=\left( m+1 \right){{x}^{3}}-\left( 2m-1 \right){{x}^{2}}+x-1\) không có điểm cực đại?
- Cho hình trụ có 2 đáy là hai hình tròn \(\left( O \right)\) và \(\left( O' \right)\), thiết diện qua trục của hình trụ là hình vuông. Gọi \(A\) và \(B\) là 2 điểm lần lượt nằm trên hai đường tròn \(\left( O' \right)\) và \(\left( O \right)\). Biết \(AB=2a\) và khoảng cách giữa \(AB\) và \(OO'\) bằng \(\frac{a\sqrt{3}}{2}\). Tính diện tích xung quanh của hình trụ?
- Cho 2 mặt phẳng \(\left( P \right)\)và \(\left( Q \right)\) song song với nhau và cùng cắt khối cầu tâm \(O\) bán kính \(4\sqrt{3}\) thành 2 hình tròn có cùng bán kính. Xét hình nón có đỉnh trùng với tâm của một trong hai hình tròn này và có đáy là hình tròn còn lại. Khi diện tích xung quanh của hình nón là lớn nhất, khoảng cách \(h\) giữa hai mặt phẳng \(\left( P \right)\)và \(\left( Q \right)\) bằng?
- Cho khối chóp \(S.ABCD\) có đáy là hình vuông cạnh \(a,\) cạnh bên \(SA=y\,\,\left( y>0 \right).\) và
- Cho hàm số \(y=f\left( 2-x \right)\) có BBT như sau: Tổng các giá trị nguyên của tham số \(m\) để phương trình \(3{{f}^{2}}\left( {{x}^{2}}-4x \right)-\left( m+2 \right)f\left( {{x}^{2}}-4x \right)+m-1=0\) có đúng 8 nghiệm thực phân biệt thuộc khoảng \(\left( 0;+\infty \right)\)?
- Cho hàm số \(f\left( x \right)\) liên tục trên đoạn \(\left[ -4;\,4 \right]\) và có BBT như hình: Có tất cả bao nhiêu giá trị thực của tham số \(m\) thuộc đoạn \(\left[ -4;\,4 \right]\) để giá trị lớn nhất của hàm số \(g\left( x \right)=\left| f\left( {{x}^{3}}-3x+2 \right)+2f\left( m \right) \right|\) có giá trị lớn nhất trên đoạn \(\left[ -1;1 \right]\) bằng \(5\)?
- Cho hàm số \(y={{x}^{3}}-6{{x}^{2}}+9x+m\text{ }\left( C \right)\), với \(m\) là tham số. Giả sử đồ thị
- Có tất cả bao nhiêu số nguyên dương của tham số m để hàm số sau \(y=\frac{\cos x+1}{10\cos x+m}\) đồng biến trên khoảng \(\left( 0;\frac{\pi }{2} \right)\cdot \)?
- Cho có tháp nước như hình, tháp được thiết kế gồm thân tháp có dạng hình trụ, phần mái phía trên dạng hình nón và đáy là nửa hình cầu. Không gian bên trong toàn bộ tháp được minh họa theo hình vẽ với đường kính đáy hình trụ, hình cầu và đường kính đáy của hình nón đều bằng 3m, chiều cao hình trụ là 2m, chiều cao của hình nón là 1m. Thể tích của toán bộ không gian bên trong tháp nước gần nhất với giá trị nào sau đây?
- Gọi \(S\) là tập nghiệm của phương trình sau \(2{{\log }_{2}}\left( 2x-2 \right)+{{\log }_{2}}{{\left( x-3 \right)}^{2}}=2\) trên \(\mathbb{R}\). Tổng các phần tử của \(S\) bằng?
- Cho khối lăng trụ \(ABC.{A}'{B}'{C}'\) có \(AB=3a,\)\(AC=4a,\) \(BC=5a,\) khoảng cách giữa 2 đường thẳng \(AB\) và \({B}'{C}'\) bằng \(2a.\) Gọi \(M,\) \(N\) lần lượt là trung điểm của \({A}'{B}'\) và \({A}'{C}',\) (tham khảo hình vẽ dưới đây). Thể tích \(V\) của khối chóp \(A.BCNM\) là?
- Cho đồ thị \(\left( C \right):y=\frac{x+2}{x-1}\). Gọi \(A,\ B,\ C\) là 3 điểm phân biệt thuộc \(\left( C \right)\) sao cho trực tâm \(H\) của tam giác \(ABC\) thuộc đường thẳng \(\Delta :y=-3x+10\). Độ dài đoạn thẳng \(OH\) bằng?
- Cho khối lăng trụ \(ABC.{A}'{B}'{C}'\) có đáy \(ABC\) là tam giác vuông cân tại \(B\) và \(AC=2a\). Hình
- Có tất cả bao nhiêu cặp số nguyên \(\left( x;y \right)\) thỏa mãn \(0\le x\le 4000\) và \(5\left( {{25}^{y}}+2y \right)=x+{{\log }_{5}}{{\left( x+1 \right)}^{5}}-4\)?
- Cho hình lập phương \(ABCD.{A}'{B}'{C}'{D}'\) có cạnh bằng \(a\). Gọi \(\alpha \) là góc giữa \(\left( AC{D}' \right)\) & \(\left( ABCD \right)\). Giá trị của \(\tan \alpha \) bằng?
- Cho hình thang ABCD vuông tại A và D có \(CD=2AB=2AD=6.\) Tính thể tích V của khối tròn xoay sinh ra bởi hình thang ABCD khi quay xung quanh đường thẳng BC?
- Cho phương trình sau \(\left( 4\log _{2}^{2}x+{{\log }_{2}}x-5 \right)\sqrt{{{7}^{x}}-m}=0\) (\(m\) là tham số thực). Có tất cả bao nhiêu giá trị nguyên dương của để phương trình đã cho có đúng 2 nghiệm phân biệt?
- Một hộp có 6 viên bi xanh, 4 viên bi đỏ và 5 viên bi vàng. Chọn ngẫu nhiên 5 viên bi trong hộp,
- Cho hình chóp \(S.ABC\) có \(AB=4a,BC=3\sqrt{2}a,\) \(\widehat{ABC}=45{}^\circ ;\widehat{SAC}=\widehat{SBC}=90{}^\circ \); Sin góc giữa 2 mặt phẳng\(\left( SAB \right)\) và \(\left( SBC \right)\) bằng \(\frac{\sqrt{2}}{4}.\) Bán kính mặt cầu ngoại tiếp hình chóp đã cho bằng?
- Có tất cả bao nhiêu giá trị nguyên của tham số m để hàm số sau \(y=\left| 3{{x}^{4}}-m{{x}^{3}}+6{{x}^{2}}+m-3 \right|\) đồng biến trên khoảng \(\left( 0;+\infty \right)\)?

