Giải bài 41 tr 162 sách BT Toán lớp 9 Tập 1
Cho nửa đường tròn tâm O, đường kính AB. Qua điểm C thuộc nửa đường tròn kẻ tiếp tuyến d của đường tròn. Gọi E và F lần lượt là chân các đường vuông góc kẻ từ A và B đến d. Gọi H là chân đường vuông góc kẻ từ C đến AB. Chứng minh rằng :
a. CE = CF
b. AC là tia phân giác của góc BAE
c. CH2 = AE.BF
Hướng dẫn giải chi tiết
Hướng dẫn giải
Sử dụng kiến thức:
+) Nếu một đường thẳng là tiếp tuyến của một đường tròn thì nó vuông góc với bán kính đi qua tiếp điểm.
+) Trong tam giác vuông, bình phương đường cao ứng với cạnh huyền bằng tích hai hình chiếu của hai cạnh góc vuông lên cạnh huyền.
Lời giải chi tiết
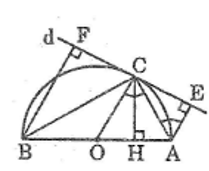
\(a)\) Ta có: \(OC ⊥d\) ( tính chất tiếp tuyến)
\(AE ⊥ d\;\; (gt)\)
\(BF ⊥ d \;\;(gt)\)
Suy ra: \(OC // AE // BF \;\;(*)\)
Mà \(OA = OB (=R)\)
Suy ra: \( CE = CF\) (tính chất đường thẳng song cách đều)
\(b)\) Ta có: \(AE // OC\) (theo \((*)\))
Suy ra: \(\widehat {OCA} = \widehat {EAC}\) ( hai góc so le trong) \((1)\)
Ta có: \(OA = OC (=R)\)
Suy ra: \(∆OAC\) cân tại \(O\) \( \Rightarrow \widehat {OCA} = \widehat {OAC}\) \((2)\)
Từ \((1)\) và \((2)\) suy ra: \(\widehat {EAC} = \widehat {OAC}\)
Vậy \(AC\) là tia phân giác của góc \(OAE\) hay \(AC\) là tia phân giác của góc \(BAE.\)
\(c)\) Tam giác \(ABC\) nội tiếp trong đường tròn \((O)\) có \(AB\) là đường kính nên \(\widehat {ACB} = 90^\circ \)
Tam giác \(ABC\) vuông tại \(C\) có \(CH ⊥ AB.\)
Theo hệ thức liên hệ giữa đường cao và hình chiếu, ta có:
\(C{H^2} = HA.HB\;\; (3)\)
Xét hai tam giác \(ACH\) và \(ACE,\) ta có:
+) \(\widehat {AEC} = \widehat {AHC} = 90^\circ \)
+) \(CH = CE\) (tính chất đường phân giác)
+) \(AC\) chung
Suy ra: \(∆ACH = ∆ACE\) (cạnh huyền, cạnh góc vuông)
Suy ra: \(AH = AE\;\;(4)\)
Xét hai tam giác \(BCH\) và \(BEF,\) ta có:
+) \(\widehat {BHC} = \widehat {BFC} = 90^\circ \)
+) \(CH = CF (= CE)\)
+) \(BC \) chung
Suy ra: \(∆BCH = ∆BCF\) (cạnh huyền, cạnh góc vuông)
Suy ra: \(BH = BF \;\;(5)\)
Từ \((3),\) \((4)\) và \((5)\) suy ra: \(C{H^2} = AE.BF\)
-- Mod Toán 9 HỌC247
Bài tập SGK khác
-


Bài 35 trang 162 sách bài tập toán 9 tập 1
bởi Lê Văn Duyệt
 10/10/2018
10/10/2018
Bài 35 (Sách bài tập trang 162)
Trên mặt phẳng tọa độ cho điểm I có tọa độ (-3; 2). Nếu vẽ đường tròn tâm I bán kính bằng 2 thì đường tròn đó có vị trí tương đối như thế nào đối với trục tọa độ ?
Theo dõi (0) 1 Trả lời -


Chứng minh AB^2=BD.BE biết hai đường tròn (O) và (O') cắt nhau tại A và B
bởi sggr sgbrthr
 12/01/2018
12/01/2018
Cho hai đường tròn (O) và (O') cắt nhau tại A và B. Qua A vẽ tiếp tuến Ax với (O) nó cắt đường tròn (O') tại E. Qua A vẽ tiếp tuyến Ay với (O') nó cắt đường tròn (O) tại D. Chứng minh: AB2=BD.BE
Theo dõi (1) 1 Trả lời





