Giải bài 4.2 tr 163 sách BT Toán lớp 9 Tập 1
Cho đường tròn (O; 2cm), điểm A di chuyển trên đường tròn. Trên tiếp tuyến tại A, lấy điểm M sao cho AM = OA. Điểm M chuyển động trên đường nào?
Hướng dẫn giải chi tiết
Hướng dẫn giải
Sử dụng kiến thức: Tập hợp tất cả các điểm cách một điểm cố định \(O\) một khoảng không đổi \(r\) là đường tròn tâm \(O\), bán kính \(r.\)
Lời giải chi tiết
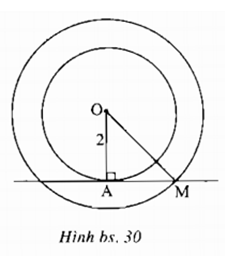
Vì AM là tiếp tuyến của đường tròn (O) nên \(AM\bot OA\).
Lại có \(AM=OA=2cm\) nên \(\Delta OAM\) là tam giác vuông cân tại \(A\)
Theo định lý Pytago ta có: \(O{M^2} = O{A^2} + A{M^2} \)\(= {2^2} + {2^2} = 8\)
\(\Rightarrow OM = 2\sqrt 2 \).
Do điểm \(O\) cố định nên điểm \(M\) chuyển động trên đường tròn \((O ; 2\sqrt 2 cm).\
-- Mod Toán 9 HỌC247
Bài tập SGK khác
Chưa có câu hỏi nào. Em hãy trở thành người đầu tiên đặt câu hỏi.





