Bài tập 33 trang 105 SBT Toán 9 Tập 2

Hướng dẫn giải

Muốn chứng minh quỹ tích (tập hợp) các điểm \(M\) thỏa mãn tính chất \(\tau\) là một hình \({\rm H}\) nào đó, ta phải chứng minh hai phần:

Phần thuận: Mọi điểm có tính chất \(\tau\) đều thuộc hình \(\rm H.\)

Phần đảo: Mọi điểm thuộc hình \(\rm H\) đều có tính chất \(\tau.\)

Kết luận: Quỹ tích (hay tập hợp) các điểm \(M\) có tính chất \(\tau\) là hình \(\rm H.\)

(Thông thường với bài toán "Tìm quỹ tích..." ta nên dự đoán hình \(\rm H\) trước khi chứng minh: Tập hợp các điểm \(M\) tạo với hai mút của đoạn thẳng \(AB\) cho trước một góc \(AMB\) bằng \(\alpha\) \((\alpha\) không đổi \()\) là hai cung tròn đối xứng với nhau qua \(AB\) (gọi là cung chứa góc \(\alpha\) vẽ trên đoạn \(AB\))).

Lời giải chi tiết

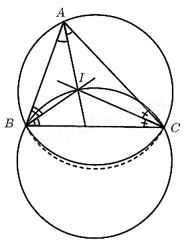
Chứng minh thuận:

Gọi \(I\) là giao điểm \(3\) đường phân giác trong của \(∆ABC\)

\(\widehat {IBC} =\displaystyle {{\widehat B} \over 2};\) \(\widehat {ICB} = \displaystyle {{\widehat C} \over 2}\)

\( \Rightarrow \) \(\widehat {IBC} + \widehat {ICB} = \displaystyle {{\widehat B + \widehat C} \over 2}\) mà trong \(∆ABC\) ta có: \(\widehat B + \widehat C = 180^\circ  - \widehat A = 180^\circ  - \alpha \)

Suy ra: \(\widehat {IBC} + \widehat {ICB} =\displaystyle  {{180^\circ  - \alpha } \over 2}\)

Trong \(∆BIC\) ta có: \(\widehat {BIC} = 180^\circ  - (\widehat {IBC} + \widehat {ICB})\)

Suy ra: \(\widehat {BIC} = \displaystyle  180^\circ  - {{180^\circ  - \alpha } \over 2}\)\( = \displaystyle {{360^\circ  - 180^\circ  + \alpha } \over 2}\)\( =\displaystyle  90^\circ  + {\alpha  \over 2}\)

Do \(\widehat Α=\alpha\) không đổi \( \Rightarrow \widehat {BIC} = 90^\circ  + \displaystyle {\alpha  \over 2}\) không đổi.

Vì \(I\) thay đổi tạo với \(2\) đầu đoạn \(BC\) cố định một góc bằng \(90^\circ + \displaystyle {\alpha  \over 2}\) không đổi

Do đó, \(I\) nằm trên cung chứa góc \(90^\circ + \displaystyle {\alpha  \over 2}\) vẽ trên \(BC.\)

Chứng minh đảo:  Trên cung chứa góc \(90^\circ + \displaystyle {\alpha  \over 2}\) lấy điểm \(I’ \) bất kỳ. Vẽ trên cùng nửa mặt phẳng bờ \(BC\) chứa điểm \(I’\) hai tai \(Bx\) và \(Cy\) sao cho \(BI’\) là phân giác của \(\widehat {CBx},CI'\) là phân giác của \(\widehat {BCy}\).

\(Bx\) cắt \(Cy\) tại \(A'.\)

Trong \(∆BI'C\) ta có: \(\widehat {BI'C} = 90^\circ + \displaystyle {\alpha  \over 2}\)

\( \Rightarrow \widehat {I'BC} + \widehat {I'CB} = 180^\circ  - \widehat {BI'C}\)\( =\displaystyle 180^\circ  - \left( {90^\circ  + {\alpha  \over 2}} \right)\)\( = \displaystyle {{180^\circ  - \alpha } \over 2}\)

\(\widehat {CBA'} = 2\widehat {I'BC};\widehat {BCA'} = 2\widehat {I'CB}\)

\( \Rightarrow \widehat {CBA'} + \widehat {BCA'} =\displaystyle  2.{{180^\circ  - \alpha } \over 2} \)\(= 180^\circ  - \alpha \)

Trong \(∆A'BC\) ta có:

\(\widehat {BA'C} = 180^\circ  - (\widehat {CBA'} + \widehat {BCA'}) \)\(= 180^\circ  - (180^\circ  - \alpha ) = \alpha \)

Kết luận: Vậy quỹ tích giao điểm \(3\) đường phân giác trong \(∆ABC\) khi \(\widehat A = \alpha \) không đổi, \(BC\) cố định là \(2\) cung chứa góc \(90^\circ  + \displaystyle {\alpha  \over 2}\) vẽ trên \(BC.\)

-- Mod Toán 9 HỌC247