Giải bài 38 tr 12 sách BT Toán lớp 8 Tập 2
Giải các phương trình sau:
a. \({{1 - x} \over {x + 1}} + 3 = {{2x + 3} \over {x + 1}}\)
b. \({{{{\left( {x + 2} \right)}^2}} \over {2x - 3}} - 1 = {{{x^2} + 10} \over {2x - 3}}\)
c. \({{5x - 2} \over {2 - 2x}} + {{2x - 1} \over 2} = 1 - {{{x^2} + x - 3} \over {1 - x}}\)
d. \({{5 - 2x} \over 3} + {{\left( {x - 1} \right)\left( {x + 1} \right)} \over {3x - 1}} = {{\left( {x + 2} \right)\left( {1 - 3x} \right)} \over {9x - 3}}\)
Hướng dẫn giải chi tiết
Hướng dẫn giải
Giải phương trình chứa ẩn ở mẫu
Bước 1: Tìm điều kiện xác định của phương trình.
Bước 2: Quy đồng mẫu hai vế của phương trình rồi khử mẫu.
Bước 3: Giải phương trình vừa nhận được.
Bước 4: Kết luận.
Trong các giá trị của ẩn tìm được ở bước 3, các giá trị thỏa mãn điều kiện xác định chính là các nghiệm của phương trình đã cho.
Lời giải chi tiết
a. \({{1 - x} \over {x + 1}} + 3 = {{2x + 3} \over {x + 1}}\) ĐKXĐ: \(x \ne - 1\)
\(\eqalign{ & \Leftrightarrow {{1 - x} \over {x + 1}} + {{3\left( {x + 1} \right)} \over {x + 1}} = {{2x + 3} \over {x + 1}} \cr & \Leftrightarrow 1 - x + 3\left( {x + 1} \right) = 2x + 3 \cr & \Leftrightarrow 1 - x + 3x + 3 - 2x - 3 = 0 \cr & \Leftrightarrow 0x = - 1 \cr} \)
Phương trình vô nghiệm.
b. \({{{{\left( {x + 2} \right)}^2}} \over {2x - 3}} - 1 = {{{x^2} + 10} \over {2x - 3}}\)
ĐKXĐ: \(x \ne {3 \over 2}\)
\(\eqalign{ & \Leftrightarrow {{{{\left( {x + 2} \right)}^2}} \over {2x - 3}} - {{2x - 3} \over {2x - 3}} = {{{x^2} + 10} \over {2x - 3}} \cr & \Leftrightarrow {\left( {x + 2} \right)^2} - \left( {2x - 3} \right) = {x^2} + 10 \cr & \Leftrightarrow {x^2} + 4x + 4 - 2x + 3 - {x^2} - 10 = 0 \cr & \Leftrightarrow 2x = 3 \cr} \)
\( \Leftrightarrow x = {3 \over 2}\) (loại)
Phương trình vô nghiệm.
c. \({{5x - 2} \over {2 - 2x}} + {{2x - 1} \over 2} = 1 - {{{x^2} + x - 3} \over {1 - x}}\)
ĐKXĐ: \(x \ne 1\)
\(\eqalign{ & \Leftrightarrow {{5x - 2} \over {2\left( {1 - x} \right)}} + {{\left( {2x - 1} \right)\left( {1 - x} \right)} \over {2\left( {1 - x} \right)}} = {{2\left( {1 - x} \right)} \over {2\left( {1 - x} \right)}} - {{2\left( {{x^2} + x - 3} \right)} \over {2\left( {1 - x} \right)}} \cr & \Leftrightarrow 5x - 2 + \left( {2x - 1} \right)\left( {1 - x} \right) = 2\left( {1 - x} \right) - 2\left( {{x^2} + x - 3} \right) \cr & \Leftrightarrow 5x - 2 + 2x - 2{x^2} - 1 + x - 2 + 2x + 2{x^2} + 2x - 6 = 0 \cr & \Leftrightarrow 5x + 2x + x + 2x + 2x = 2 + 6 + 2 + 1 \Leftrightarrow 12x = 11 \cr} \)
\( \Leftrightarrow x = {{11} \over {12}}\) (thỏa)
Vậy phương trình có nghiệm \(x = {{11} \over {12}}\)
d. \({{5 - 2x} \over 3} + {{\left( {x - 1} \right)\left( {x + 1} \right)} \over {3x - 1}} = {{\left( {x + 2} \right)\left( {1 - 3x} \right)} \over {9x - 3}}\) ĐKXĐ: \(x \ne {1 \over 3}\)
\(\eqalign{ & \Leftrightarrow {{\left( {5 - 2x} \right)\left( {3x - 1} \right)} \over {3\left( {3x - 1} \right)}} + {{3\left( {x + 1} \right)\left( {x - 1} \right)} \over {3\left( {3x - 1} \right)}} = {{\left( {x + 2} \right)\left( {1 - 3x} \right)} \over {3\left( {3x - 1} \right)}} \cr & \Leftrightarrow \left( {5 - 2x} \right)\left( {3x - 1} \right) + 3\left( {x + 1} \right)\left( {x - 1} \right) = \left( {x + 2} \right)\left( {1 - 3x} \right) \cr & \Leftrightarrow 15x - 5 - 6{x^2} + 2x + 3{x^2} - 3 = x - 3{x^2} + 2 - 6x \cr & \Leftrightarrow - 6{x^2} + 3{x^2} + 3{x^2} + 15x + 2x - x + 6x = 2 + 5 + 3 \cr & \Leftrightarrow 22x = 10 \cr} \)
\( \Leftrightarrow x = {5 \over {11}}\) (thỏa)
Vậy phương trình có nghiệm \(x = {5 \over {11}}\)
-- Mod Toán 8 HỌC247
Bài tập SGK khác
-


Giải phương trình 1/x-2/(x+1)=3/(x^2+x)
bởi ZinnZinn
 29/02/2020
29/02/2020
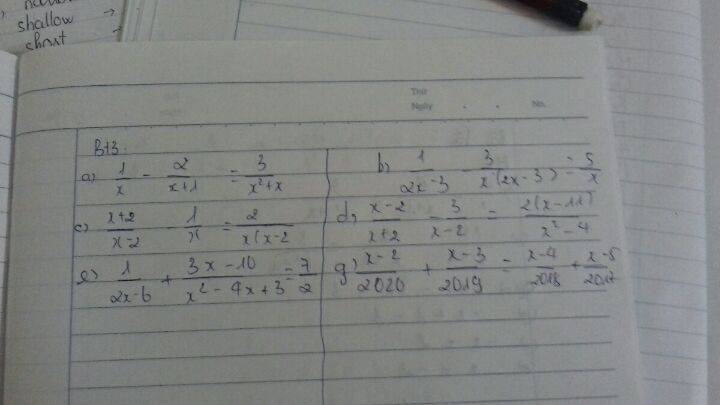 Theo dõi (0) 1 Trả lời
Theo dõi (0) 1 Trả lời -

 Giải phương trình bài 2
Giải phương trình bài 2 Theo dõi (0) 0 Trả lời
Theo dõi (0) 0 Trả lời -


Giải phương trình x+1/x+2=3
bởi Phạm Tuân
 26/02/2020
giải phương trình:a)x 1/x 2=3b)7-2x/x-1=1-4x/x-23-2x/x 1=2 1-4x/x-2Theo dõi (0) 0 Trả lời
26/02/2020
giải phương trình:a)x 1/x 2=3b)7-2x/x-1=1-4x/x-23-2x/x 1=2 1-4x/x-2Theo dõi (0) 0 Trả lời -


Cho hình thang ABCD (AB//CD, AB
bởi Thảo Thảo
 25/02/2020
Bài 1nha
25/02/2020
Bài 1nha Theo dõi (0) 3 Trả lời
Theo dõi (0) 3 Trả lời -
ADMICRO


Tìm x biết (4x-5)((6x-1)/3+1)=0
bởi Yorn Nguyễn
 23/02/2020
Giúp mình vs ạ, đang cần gấp
23/02/2020
Giúp mình vs ạ, đang cần gấp Theo dõi (0) 1 Trả lời
Theo dõi (0) 1 Trả lời -


Tìm x biết x-3/x-2 - x-7/x-4 = 3+ 1/5
bởi Va'an Va'an
 22/02/2020
22/02/2020
Giải pt chứa ẩn ở mẫu
Theo dõi (0) 1 Trả lời -


Giải phương trình chứa ẩn ở mẫu 1/x-1+1=1/x-1
bởi Nguyễn Thu Hiền
 22/02/2020
Giải các phương trình chứa ẩn ở mẫu saux-1/x-1 1=1/x-1Theo dõi (0) 0 Trả lời
22/02/2020
Giải các phương trình chứa ẩn ở mẫu saux-1/x-1 1=1/x-1Theo dõi (0) 0 Trả lời -


Giải phương trình x+1/x-2 x-1/x+2 = 2(x^2+2)/x^2-4
bởi Kim Ngân Hoàng
 21/02/2020
x 1/x-2 x-1/x 2 = 2(x^2 2)/x^2-4
21/02/2020
x 1/x-2 x-1/x 2 = 2(x^2 2)/x^2-4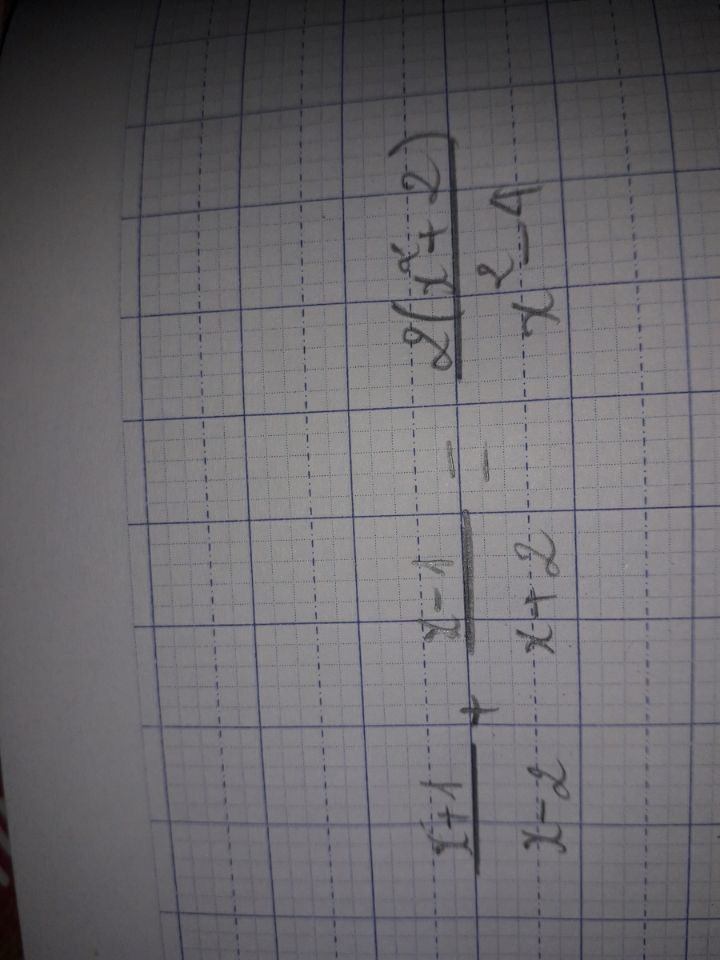 Theo dõi (0) 4 Trả lời
Theo dõi (0) 4 Trả lời -


Rút gọn A=(1/(x-2)-2x/(4-x^2)_1/(2+x)).(2/x-1)
bởi Hanh Vu Bich
 17/02/2020
17/02/2020
 Theo dõi (0) 2 Trả lời
Theo dõi (0) 2 Trả lời -


Tử của phân số lớn hơn mẫu của nó của nó 5 đơn vị. Nếu ta thêm vào tử 17 đơn vị và vào mẫu 2 đơn vị thì được một phân số mới bang số nghịch đảo của phân số ban đầu. Tìm phân số ban đầu.
bởi Phan Hằng
 15/02/2020
15/02/2020
 Theo dõi (0) 0 Trả lời
Theo dõi (0) 0 Trả lời -


Giải phuơng trình x-1/3+1=x-2/2+2
bởi Xuyến Trần
 15/02/2020
Giải giúp em vs ạTheo dõi (0) 0 Trả lời
15/02/2020
Giải giúp em vs ạTheo dõi (0) 0 Trả lời -


Giải phương trình (x-1)/x+1/(x+1)=(2x-1)/(2x^2+2)
bởi Như Mai
 11/02/2020
11/02/2020
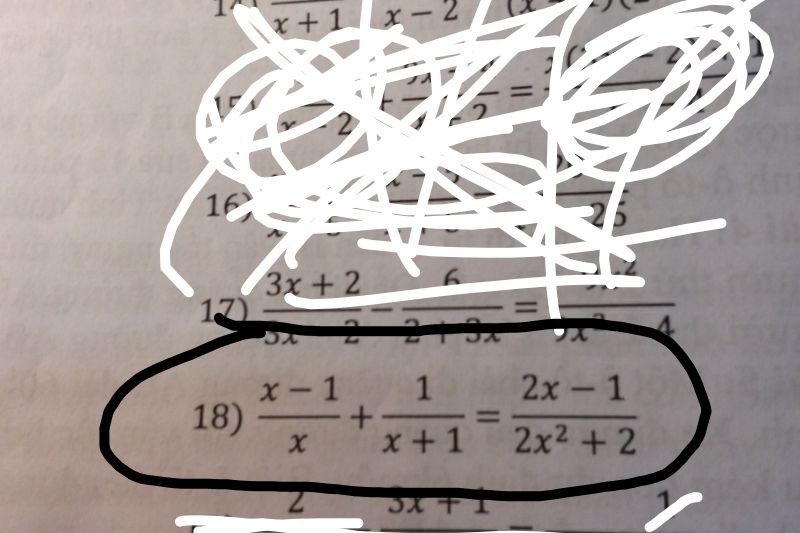 Theo dõi (0) 0 Trả lời
Theo dõi (0) 0 Trả lời -


Giải phương trình x/(x-3)-x/(x-5)=x/(x-4)-x/(x-6)
bởi Bóng Đèn Nhỏ
 11/02/2020
11/02/2020
Giải phương trình:
Theo dõi (0) 3 Trả lời -


Giải phương trình (2x-3)(3x+4)=0
bởi Lãnh Hàn Bảo Nam
 09/02/2020
Cho mk hỏi bài 1 ạ
09/02/2020
Cho mk hỏi bài 1 ạ Theo dõi (0) 3 Trả lời
Theo dõi (0) 3 Trả lời -


Giải phương trình x-1+2/x^2 x 1=3x^2/x^2-1
bởi Thanhtam Le
 06/02/2020
1/x-1 2/x^2 x 1=3x^2/x^2-1Theo dõi (1) 1 Trả lời
06/02/2020
1/x-1 2/x^2 x 1=3x^2/x^2-1Theo dõi (1) 1 Trả lời -


Giải phương trình (x-2)(3x+5)=(2x-4)(x+1)
bởi An Nguyễn
 06/02/2020
Giúp mình bài 4 với
06/02/2020
Giúp mình bài 4 với Theo dõi (0) 1 Trả lời
Theo dõi (0) 1 Trả lời -


x+1/2004 + x+2/2003= x+3/ 2002+ x+1/2001
Theo dõi (1) 5 Trả lời -


Giải phương trình 2x/x+1 +18/x2+2x-3=2x-5/x+3
bởi Vũ Nhược Ann
 29/01/2020
29/01/2020
2x/x+1 +18/x2+2x-3=2x-5/x+3
Theo dõi (0) 1 Trả lời -


Giải phương trình 2/x^2+3x 2+1/x^2 5x+6 = 1/x^2-3x+2
bởi Anna
 08/01/2020
2/x^2 3x 2 1/x^2 5x 6 = 1/x^2-3x 2Theo dõi (0) 0 Trả lời
08/01/2020
2/x^2 3x 2 1/x^2 5x 6 = 1/x^2-3x 2Theo dõi (0) 0 Trả lời -


Giải phương trình 1/x+2=(1/x+2)(x^2+1)
bởi nguyễn khánh linh
 04/01/2020
Bài tập 32 sgk toán 8 tập 2
04/01/2020
Bài tập 32 sgk toán 8 tập 2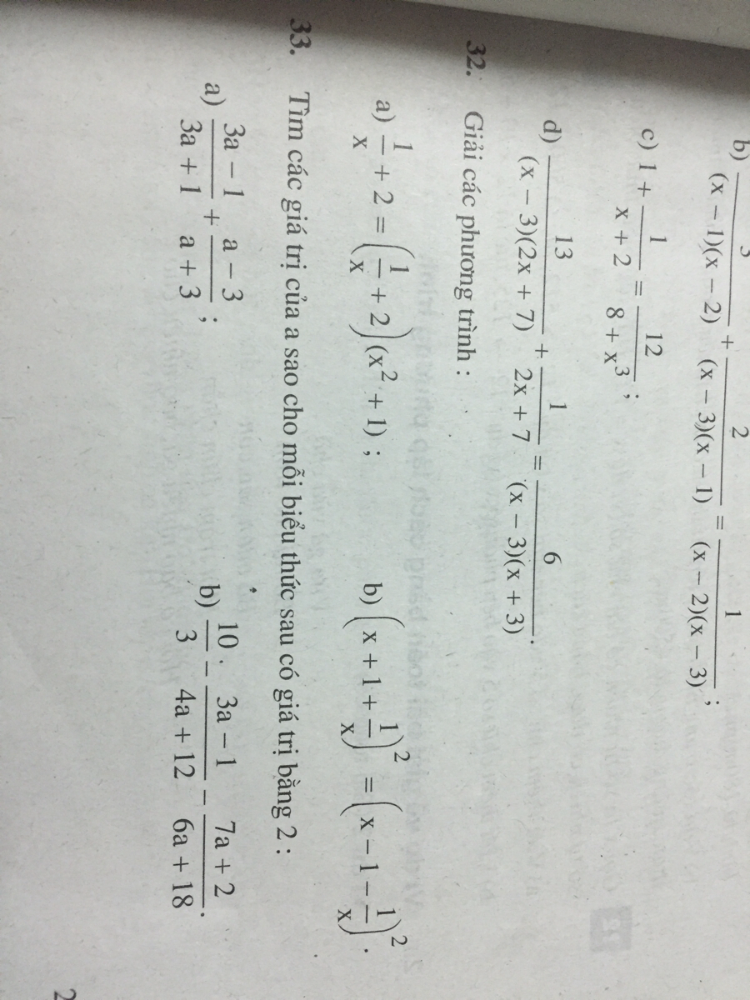 Theo dõi (0) 0 Trả lời
Theo dõi (0) 0 Trả lời -


Tìm m phương trình sau nhận x = 3 làm nghiệm
(m2 - 1) x + 3 = 2m + 1
Theo dõi (0) 1 Trả lời -


Giải phương trình x+3/x+1+x−2/x=2
bởi Bo Bo
 25/02/2019
25/02/2019
Giải các PT
\(\dfrac{x+3}{x+1}+\dfrac{x-2}{x}=2\)
Theo dõi (0) 2 Trả lời -


Tìm x biết 5-4x=3x-9
bởi Nguyễn Minh Minh
 26/12/2018
26/12/2018
a) 5-4x=3x-9
b) (x-4)(3x+9)=0
c) (x/(x+4))+(12/(x-4))=(4x+48)/(x*x-16)
d) 4-2x=7-x
e) (x+4)(8-4x)=0
f) (x/(x+5))+(11/(x-5))=(x+55)/(x*x-25)
g) ((3x+2)/2) - ((3x+1)/6)= (5/3) +2x
h) 2x-(3-5x)=4(x+3)
i) 3x -6+x=9-x
k) 2t-3+5t= 4t+12
m.n giúp mik ạ ...
Theo dõi (0) 1 Trả lời -


Tìm x biết 8x/x-7-8=1/x-7
bởi Tieu Dong
 26/12/2018
26/12/2018
8x trên x-7 trừ 8 =1 trên x-7
Theo dõi (0) 1 Trả lời -


Giải phương trình x^2+(x/x+1)^2=5/4
bởi Nguyễn Thanh Hà
 29/01/2019
29/01/2019
giải phương trình:\(x^2+\left(\dfrac{x}{x+1}\right)^2=\dfrac{5}{4}\)
Theo dõi (0) 1 Trả lời -


Giải bất phương trình 1/3-5x > 1/2x+3
bởi Anh Nguyễn
 27/12/2018
27/12/2018
Giải các bất phương trình sau:
a)\(\dfrac{1}{3-5x}>\dfrac{1}{2x+3}\)
Theo dõi (0) 1 Trả lời -


Giải phương trình 3x-2=2x-3
bởi Anh Nguyễn
 31/12/2018
31/12/2018
Giải các phương trình
a)3x-2=2x-3 c)11x+42-2x=100-9x-22
b)2x+3=5x+9 d)2x-(3-5x)=4(x+3)
e)\(\dfrac{3x+2}{2}-\dfrac{3x+1}{6}=\dfrac{5}{3}+2x\)
f)\(\dfrac{x+4}{5}-x+4=\dfrac{x}{3}-\dfrac{x-2}{2}\)
g)(2x+1)(x-1)=0
h)(x+\(\dfrac{2}{3}\))(x-\(\dfrac{1}{2}\))=0
i)(3x-1)(2x-3)(2x-3)(x+5)=0
k)3x-15=2x(x-5)
m)\(\left|x-2\right|=3\)
n)\(\left|x+1\right|=\left|2x+3\right|\)
j)\(\dfrac{7x-3}{x-1}=\dfrac{2}{3}\)
đ)\(\dfrac{2\left(3-7x\right)}{1+x}=\dfrac{1}{2}\)
y)\(\dfrac{x+5}{x-5}-\dfrac{x-5}{x+5}=\dfrac{20}{x^2-25}\)
\(\dfrac{1}{x-1}+\dfrac{2}{x+1}=\dfrac{x}{x^2-1}\)
Theo dõi (0) 1 Trả lời -


I : Chứng tỏ biểu thức sau không phụ thuộc vào biến
A= 2(2x+x^2)-x^2(x+2)+x(x^2-4)
Theo dõi (0) 1 Trả lời -


Giải bất phương trinh (m^2-m-1)x-5m > (3-m)x
bởi Nguyễn Lê Thảo Trang
 29/01/2019
29/01/2019
Giả bất phương trinh:
(m2-m-1)x-5m > (3-m)x
Theo dõi (0) 1 Trả lời -


Tìm a, b để x^4-9x^3+ax^2+x+b chia hết cho x^2-x-2
bởi Nguyễn Lệ Diễm
 30/01/2019
30/01/2019
Xác định hệ số a,b,c biết :
a) \(x^4-9x^3+ax^2+x+b\) chia hết cho \(x^2-x-2\)
b) \(x^3+ax+b\) chia cho \(x+1\) thì dư 7 và khi chia cho x-3 thì dư -5
c) \(ax^3+bx^2+c\) chia hết cho x+2 và chia cho \(x^2-1\) thì dư x+5
Theo dõi (0) 1 Trả lời -


Giải phương trình x^2−y^2+2x−4y−10=
bởi Lê Chí Thiện
 30/01/2019
30/01/2019
Giải phương trình:
a) \(\dfrac{3}{x^2+5x+4}\)+\(\dfrac{2}{x^2+10x+24}\)=\(\dfrac{4}{3}\)+\(\dfrac{9}{x^2+3x-18}\)
b) x2\(-\)y2+2x\(-\)4y\(-\)10=0 (x; y ∈ N*)
Theo dõi (0) 1 Trả lời


