Giải bài 37 tr 11 sách BT Toán lớp 8 Tập 2
Các khẳng định sau đây đúng hay sai:
a) Phương trình \(\displaystyle{{4x - 8 + \left( {4 - 2x} \right)} \over {{x^2} + 1}} = 0\) có nghiệm là \(x = 2\).
b) Phương trình \(\displaystyle{{\left( {x + 2} \right)\left( {2x - 1} \right) - x - 2} \over {{x^2} - x + 1}} = 0\) có tập nghiệm là \(S = \{ -2; 1 \}\).
c) Phương trình \(\displaystyle{{{x^2} + 2x + 1} \over {x + 1}} = 0\) có nghiệm là \(x = -1\).
d) Phương trình \(\displaystyle{{{x^2}\left( {x - 3} \right)} \over x} = 0\) có tập nghiệm là \(S = \{ 0; 3 \}\).
Hướng dẫn giải chi tiết
Hướng dẫn giải
Giải phương trình chứa ẩn ở mẫu
Bước 1: Tìm điều kiện xác của phương trình.
Bước 2: Quy đồng mẫu hai vế của phương trình rồi khử mẫu.
Bước 3: Giải phương trình vừa nhận được.
Bước 4: Kết luận.
Trong các giá trị của ẩn tìm được ở bước 3, các giá trị thỏa mãn điều kiện xác định chính là các nghiệm của phương trình đã cho.
Lời giải chi tiết
a) Vì \(\displaystyle{x^2} + 1 > 0\) với mọi \(x\) nên phương trình đã cho tương đương với phương trình :
\(\displaystyle4x - 8 + \left( {4 - 2x} \right) = 0 \)
\(\displaystyle\Leftrightarrow 2x - 4 = 0 \Leftrightarrow 2x = 4 \Leftrightarrow x = 2\).
Vậy khẳng định đã cho là đúng.
b) Vì \(\displaystyle{x^2} - x + 1 =x^2-2.x.\dfrac{1}{2}+\dfrac{1}{4}+\dfrac{3}{4}\)\(\displaystyle = {\left( {x - {1 \over 2}} \right)^2} + {3 \over 4} > 0\) với mọi \(x\) nên phương trình đã cho tương đương với phương trình:
\(\displaystyle\left( {x + 2} \right)\left( {2x - 1} \right) - x - 2 = 0 \)
\(\displaystyle \Leftrightarrow \left( {x + 2} \right)\left( {2x - 1} \right) - (x + 2) = 0 \)
\(\displaystyle \Leftrightarrow \left( {x + 2} \right)\left( {2x - 2} \right)=0\)
\(\displaystyle \Leftrightarrow x + 2 = 0\) hoặc \(\displaystyle 2x - 2 = 0\)
\(\displaystyle \Leftrightarrow x = - 2\) hoặc \(\displaystyle 2x = 2\)
\(\displaystyle \Leftrightarrow x = - 2\) hoặc \(\displaystyle x = 1\)
Vậy khẳng định đã cho là đúng.
c) Điều kiện xác định của phương trình là \(\displaystyle x + 1 \ne 0\) \(\displaystyle \Leftrightarrow x \ne - 1\)
Do vậy phương trình \(\displaystyle{{{x^2} + 2x + 1} \over {x + 1}} = 0\) không thể có nghiệm \(\displaystyle x = -1\).
Vậy khẳng định đã cho là sai.
d) Điều kiện xác định của phương trình là \(\displaystyle x \ne 0\).
Do vậy \(x = 0\) không phải là nghiệm của phương trình \(\displaystyle{{{x^2}\left( {x - 3} \right)} \over x} = 0\).
Vậy khẳng định đã cho là sai.
-- Mod Toán 8 HỌC247
Bài tập SGK khác
-


giúp mk với mk chả hiểu đề
Theo dõi (1) 9 Trả lời -


Giải phương trình x+3/x-4 x-1/x-2=2/6x-8-x^2
bởi Linh Linh
 05/04/2020
05/04/2020
Giải phương trình x+3/x-4 x-1/x-2=2/6x-8-x^2
Theo dõi (0) 3 Trả lời -


Giải phương trình (x+1)/9+(x+2)/8=(x+3)/7+(x+4)/6
bởi Tiên Võ
 05/04/2020
x 1/9 x 2/8 x 3/7 x 4/6
05/04/2020
x 1/9 x 2/8 x 3/7 x 4/6 Theo dõi (0) 2 Trả lời
Theo dõi (0) 2 Trả lời -


Giải phương trình x+1/9+x+2/8=x+3/7 +x+4/6
bởi Tiên Võ
 05/04/2020
05/04/2020
Giải phương trình x+1/9+x+2/8=x+3/7 +x+4/6
Theo dõi (0) 0 Trả lời -
ADMICRO


Giải phương trình (3x-2)/(x+1)=2
bởi Nguyễn Lương
 04/04/2020
Giải phương trình
04/04/2020
Giải phương trình Theo dõi (0) 8 Trả lời
Theo dõi (0) 8 Trả lời -


Giải phương trình 9x-16- x(3x+16)=0
bởi Ngu Ba kha
 04/04/2020
04/04/2020
9x-16- x(3x+16)=0
Theo dõi (0) 1 Trả lời -


2x+4+...+2016+2018/1019090 = -3x^2-4x
Theo dõi (0) 1 Trả lời -


Chứng minh rằng giá trị của A = (4x - 1 )(x - 2 ) là một số chính phương với mọi x
bởi Nguyễn Diễm
 03/04/2020
03/04/2020
Chứng minh rằng giá trị của A = (4x - 1 )(x - 2 ) là một số chính phương với mọi x
Theo dõi (0) 1 Trả lời -


Một xe đạp đi từ A đến B với v=50km/h. Sau khi đi được 30 phút thì gặp đường xấu nên quãng đường còn lại vận tốc giảm còn 35km/h vì vậy đến B chậm 18 phút so với dự đinh Tinh quãng đường AB?
bởi Diep Rose
 03/04/2020
Một xe đạp đi từ A đến B với v=50km/h.Saukhi đi được 30p thì gặp đuong xấu nên quang đg còn lại van tốc giảm còn 35km/h vì vậy đen B chậm 18p so vs dự đinh Tinh Sab?Theo dõi (1) 5 Trả lời
03/04/2020
Một xe đạp đi từ A đến B với v=50km/h.Saukhi đi được 30p thì gặp đuong xấu nên quang đg còn lại van tốc giảm còn 35km/h vì vậy đen B chậm 18p so vs dự đinh Tinh Sab?Theo dõi (1) 5 Trả lời -


Một ô tô chở hàng từ Hà Nội về Thanh Hóa với vận tốc 40km/h. Đi được nửa đường để đến Thanh Hóa kịp thời gian qui định, xe tăng vận tốc thêm 20km/h nữa. Đến Thanh Hóa xe ở lại 2h30' để nghỉ, trả hàng và nhận hàng khác rồi quay về Hà Nội với vận tốc 50km/h.Tổng tất cả thời gian đi trên đường và ở lại Thanh Hóa là 9h02'. Tính quãng đường Hà Nội - Thanh Hóa.
bởi Phuongg My
 03/04/2020
03/04/2020
 Một ô tô chở hàng từ Hà Nội về Thanh Hóa với vận tốc 40km/h. Đi được nửa đường để đến Thanh Hóa kịp thời gian qui định, xe tăng vận tốc thêm 20km/h nữa. Đến Thanh Hóa xe ở lại 2h30' để nghỉ, trả hàng và nhận hàng khác rồi quay về Hà Nội với vận tốc 50km/h.Tổng tất cả thời gian đi trên đường và ở lại Thanh Hóa là 9h02'. Tính quãng đường Hà Nội - Thanh Hóa. Theo dõi (0) 7 Trả lời
Một ô tô chở hàng từ Hà Nội về Thanh Hóa với vận tốc 40km/h. Đi được nửa đường để đến Thanh Hóa kịp thời gian qui định, xe tăng vận tốc thêm 20km/h nữa. Đến Thanh Hóa xe ở lại 2h30' để nghỉ, trả hàng và nhận hàng khác rồi quay về Hà Nội với vận tốc 50km/h.Tổng tất cả thời gian đi trên đường và ở lại Thanh Hóa là 9h02'. Tính quãng đường Hà Nội - Thanh Hóa. Theo dõi (0) 7 Trả lời -


Giải phương trình (x+1)^2 (x 1/x 2)^2=8
bởi Đặng Bảo
 02/04/2020
02/04/2020
(x 1)^2 (x 1/x 2)^2=8
Theo dõi (0) 0 Trả lời -


Gọi a là nghiệm của phương trình 2(x – 3) + 5x(x – 1) = 5x2. Khẳng định nào sau đây là đúng? A. a > 0. B. a < -2. C. a > -2. D. a > -3.
bởi Mai Tấn Fông
 02/04/2020
02/04/2020
Gọi a là nghiệm của phương trình 2(x – 3) + 5x(x – 1) = 5x2. Khẳng định nào sau
đây là đúng?
A. a > 0.B. a < -2.
C. a > -2.
D. a > -3.
Theo dõi (1) 18 Trả lời -


Giải phương trình (x – 2)(3x 5)=(2x–4)(x 1)
bởi Đào Quốc Dũng
 02/04/2020
(x – 2)(3x 5)=(2x–4)(x 1) Giúp mik vsTheo dõi (0) 7 Trả lời
02/04/2020
(x – 2)(3x 5)=(2x–4)(x 1) Giúp mik vsTheo dõi (0) 7 Trả lời -


Với giá trị nào của m thì phương trình m2y2 – (m – 2)y + 5 = 0 là phương trình bậc nhất một ẩn?
bởi Mai Tấn Fông
 02/04/2020
02/04/2020
Câu 1: Với giá trị nào của m thì phương trình m2y2 – (m – 2)y + 5 = 0 là phương trình
bậc nhất một ẩn?
A. m = 0.
B. m = 2.
C. m = 1.D. Với mọi số thực m.
Câu 2: Giải và biện luận phương trình: 2(mx + 5) + 5(x + m) = m.
Theo dõi (0) 4 Trả lời -


Giải phương trình (x-1)^2=4x+1
bởi Phúc Tiến
 02/04/2020
02/04/2020
(x-1)^2=4x+1
Theo dõi (0) 10 Trả lời -


Giải phương trình 3/(2-x)=5/x
bởi Oanh Lê Kiều
 31/03/2020
Giải Phương trình
31/03/2020
Giải Phương trình Theo dõi (0) 2 Trả lời
Theo dõi (0) 2 Trả lời -


Giải phương trình 2/(x+1)+4/x=2/(x^2+x)
bởi Anh Bui
 30/03/2020
30/03/2020
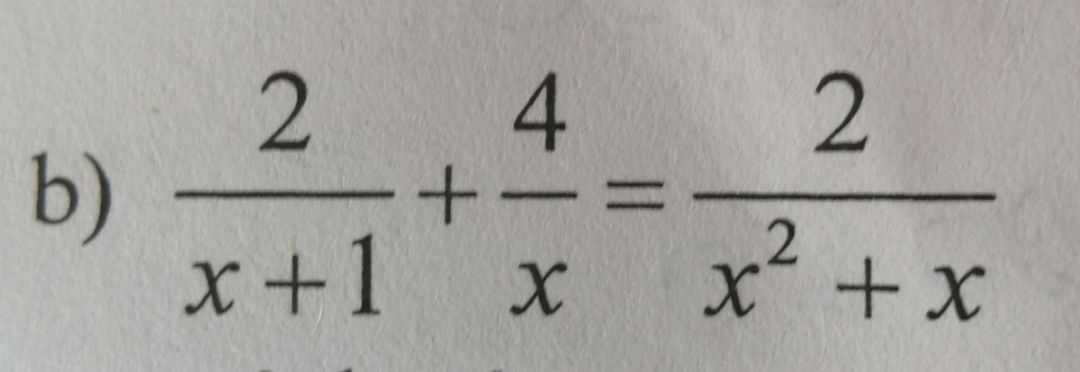 Theo dõi (1) 11 Trả lời
Theo dõi (1) 11 Trả lời -


Tìm m để phương trình (2-4m)x+3m^2-6m-9=0 vô nghiệm.
bởi Nhưý Hoàng
 27/03/2020
(2-4m)x 3m^2-6m-9=0
27/03/2020
(2-4m)x 3m^2-6m-9=0 Theo dõi (0) 1 Trả lời
Theo dõi (0) 1 Trả lời -


Giải phương trình (2x+3)/(2x-3)-3/(4x-6)=2/5
bởi Diệu Nguyễn
 26/03/2020
Giải các phương trình sau
26/03/2020
Giải các phương trình sau Theo dõi (0) 6 Trả lời
Theo dõi (0) 6 Trả lời -


Giải phương trình (x-1)^3-x(x+1)^2=5x(2-x)-11(x+2)
bởi Thanh Chung
 26/03/2020
Ở dưới
26/03/2020
Ở dưới Theo dõi (0) 4 Trả lời
Theo dõi (0) 4 Trả lời -


 Theo dõi (0) 1 Trả lời
Theo dõi (0) 1 Trả lời -


Giải phương trình 2x +5/2x-x/(x+ 5)=0
bởi Phạm Tâm
 25/03/2020
Giải phương trìnhTheo dõi (0) 1 Trả lời
25/03/2020
Giải phương trìnhTheo dõi (0) 1 Trả lời -


Tìm điều kiện xác định và rút gọn biểu thức (x+2)/x-(2x+3)/2(x-2)
bởi Lưu Nguyễn Phương Hà
 25/03/2020
25/03/2020
 Theo dõi (0) 11 Trả lời
Theo dõi (0) 11 Trả lời -


Giair phương trình 4/(x^2+2x-3)-(2x-5)/(x+3)-2x/(x-1)
bởi Hương Linh
 23/03/2020
Tl hộ mk
23/03/2020
Tl hộ mk Theo dõi (1) 2 Trả lời
Theo dõi (1) 2 Trả lời -


Tìm m để phương trình mx+1=2x-1 nhận x=2 làm nghiệm
bởi Thanh Chung
 23/03/2020
Bạn nào làm đcThì giúp mình nhéGhi hộ bài ___cách làm nhéMòng làm.sớm hộ
23/03/2020
Bạn nào làm đcThì giúp mình nhéGhi hộ bài ___cách làm nhéMòng làm.sớm hộ Theo dõi (1) 12 Trả lời
Theo dõi (1) 12 Trả lời -


 Theo dõi (1) 0 Trả lời
Theo dõi (1) 0 Trả lời -

 Cho biểu thức B =((2x 1/x-1) (8/x^2-1)-(x- 1/x 1))*(x^2-1/5) a/ Tìm điều kiện xác định của biểu thức B b/ Rút gọn biểu thức B, và chứng tỏ B > 0 với mọi x khác±1
Cho biểu thức B =((2x 1/x-1) (8/x^2-1)-(x- 1/x 1))*(x^2-1/5) a/ Tìm điều kiện xác định của biểu thức B b/ Rút gọn biểu thức B, và chứng tỏ B > 0 với mọi x khác±1 Theo dõi (0) 1 Trả lời
Theo dõi (0) 1 Trả lời -


 Theo dõi (0) 0 Trả lời
Theo dõi (0) 0 Trả lời -

 Giải phương trình
Giải phương trình Theo dõi (1) 0 Trả lời
Theo dõi (1) 0 Trả lời -


Giải phương trình 11/x=9/(x+1)+2/(x-4)
bởi Hoàng Thanh Thảo
 06/03/2020
06/03/2020
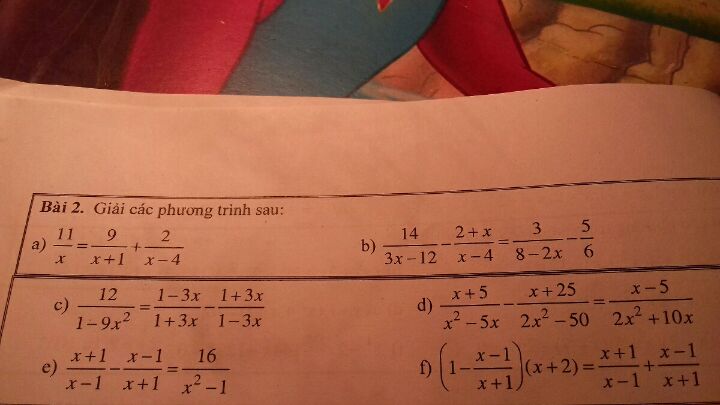 Theo dõi (0) 0 Trả lời
Theo dõi (0) 0 Trả lời -


Giải phương trình (x-1)/x+1/(x+1)=(2x-1)/(2x^2+2)
bởi Mạch Liên
 05/03/2020
Giải phương trình
05/03/2020
Giải phương trình Theo dõi (0) 0 Trả lời
Theo dõi (0) 0 Trả lời



