Bài tập 32 trang 91 SBT Toán 8 Tập 2

Hướng dẫn giải

- Nếu ba cạnh của tam giác này tỉ lệ với ba cạnh của tam giác kia thì hai tam giác đó đồng dạng.

- Tính chất: Đường trung bình tam giác thì song song với cạnh thứ ba và bằng nửa cạnh ấy.

Lời giải chi tiết

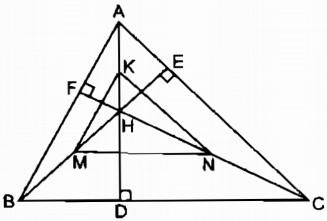
Xét \(\Delta AHB\) có:

\(K\) là trung điểm của \(AH\) (gt)

\(M\) là trung điểm của \(BH\) (gt)

Do đó \(KM\) là đường trung bình của tam giác \(AHB\).

\( \Rightarrow  \displaystyle KM  = {1 \over 2}AB\) (tính chất đường trung bình của tam giác)

\( \Rightarrow  \displaystyle {{KM} \over {AB}} = {1 \over 2}\)              (1)

Xét \(\Delta AHC\) có:

\(K\) là trung điểm của \(AH\) (gt)

\(N\) là trung điểm của \(CH\) (gt)

Do đó \(KN\) là đường trung bình của tam giác \(AHC\).

\( \Rightarrow  \displaystyle KN = {1 \over 2}AC\) (tính chất đường trung bình của tam giác)

\( \Rightarrow  \displaystyle {{KN} \over {AC}} = {1 \over 2}\)               (2)

Xét \(\Delta BHC\) có:

\(M\) trung điểm của \(BH\) (gt)

\(N\) trung điểm của \(CH\) (gt)

Do đó \(MN\) là đường trung bình của tam giác \(BHC\).

\( \Rightarrow  \displaystyle MN  = {1 \over 2}BC\) (tính chất đường trung bình của tam giác)

\( \Rightarrow  \displaystyle {{MN} \over {BC}} = {1 \over 2}\)               (3)

Từ (1), (2) và (3) suy ra: \(  \displaystyle{{KM} \over {AB}} = {{KN} \over {AC}} = {{MN} \over {BC}} = {1 \over 2}\)

Vậy \(∆ KMN\) đồng dạng \(∆ ABC\) (c.c.c).

Ta có tỉ số đồng dạng: \(\displaystyle k  = {{KM} \over {AB}} = {1 \over 2}\).

-- Mod Toán 8 HỌC247