Bài tập 142 trang 97 SBT Toán 8 Tập 1

Hướng dẫn giải

Chứng minh hình bình hành có hai đường chéo vuông góc với nhau tại trung điểm của mỗi đường là hình thoi.

Lời giải chi tiết

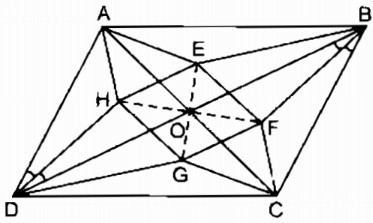
Ta có: \(\widehat {AOB} = \widehat {COD}\) (đối đỉnh)

\(\widehat {EOB} = {1 \over 2}\widehat {AOB}\) (gt)

\(\widehat {COG} = {1 \over 2}\widehat {COD}\) (gt)

Suy ra: \(\widehat {EOB} = \widehat {COG}\)

\(\widehat {EOB} + \widehat {BOC} + \widehat {COG} = 2\widehat {EOB} + \widehat {BOC}\)

mà \(\widehat {AOB} + \widehat {BOC} = {180^0}\) (kề bù)

hay \(2\widehat {EOB} + \widehat {BOC} = {180^0}\)

Suy ra: E, O, G thẳng hàng

Ta lại có: \(\widehat {BOC} = \widehat {AOD}\) (đối đỉnh)

\(\widehat {HOD} = {1 \over 2}\widehat {AOD}\) (gt)

\(\widehat {FOC} = {1 \over 2}\widehat {BOC}\) (gt)

Suy ra: \(\widehat {HOD} = \widehat {FOC}\)

\(\widehat {HOD} + \widehat {COD} + \widehat {FOC} = 2\widehat {HOD} + \widehat {COD}\)

mà \(\widehat {AOD} + \widehat {COD} = {180^0}\) (kề bù)

hay\(2\widehat {HOD} + \widehat {COD} = {180^0}\)             

Suy ra: H, O, F thẳng hàng

\(\widehat {ADO} = \widehat {CBO}\) (so le trong)

\(\widehat {HDO} = {1 \over 2}\widehat {ADO}\) (gt)

\(\widehat {FBO} = {1 \over 2}\widehat {CBO}\) (gt)

Suy ra: \(\widehat {HDO} = \widehat {FBO}\)

- Xét ∆ BFO và ∆ DHO:

\(\widehat {HDO} = \widehat {FBO}\) (chứng minh trên_

OD = OB (tính chất hình bình hành)

\(\widehat {HOD} = \widehat {FOB}\) (đối đỉnh)

Do đó: ∆ BFO = ∆ DHO (g.c.g)

⇒ OF = OH

\(\widehat {OAB} = \widehat {OCD}\) (so le trong)

\(\widehat {OAE} = {1 \over 2}\widehat {OAB}\) (gt)

\(\widehat {OCG} = {1 \over 2}\widehat {OCD}\) (gt)

Suy ra: \(\widehat {OAE} = \widehat {OCG}\)       

- Xét ∆ OAE và ∆ OCG:

\(\widehat {OAE} = \widehat {OCG}\) (chứng minh trên)

OA = OC (tính chất hình bình hành)

\(\widehat {EOA} = \widehat {GOC}\) (đối đỉnh)

Do đó: ∆ OAE = ∆ OCG (g.c.g)

⇒ OE = OG

Suy ra: Tứ giác EFGH là hình bình hành (vì có hai đường chéo cắt nhau tại trung điểm mỗi đường)

OE ⊥ OF (tính chất hai góc kề bù)

hay EG ⊥ FH

Vậy: Tứ giác EFGH là hình thoi.

-- Mod Toán 8 HỌC247