Giải bài 4.37 trang 66 SBT Toán 7 Kết nối tri thức tập 1
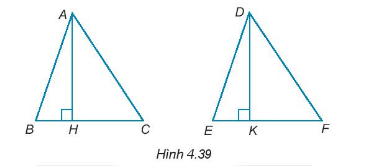
Cho AH và DK lần lượt là hai đường cao của tam giác ABC và DEF như Hình 4.39. Chứng minh rằng
a) Nếu AB = DE, BC = EF và AH = DK thì \(\Delta ABC = \Delta DEF;\)
b) Nếu AB = DE, AC = DF và AH = DK thì \(\Delta ABC = \Delta DEF\)
Hướng dẫn giải chi tiết
Phương pháp giải:
a)
-Chứng minh \(\Delta HAB = \Delta KDE\left( {ch - cgv} \right)\)
-Chứng minh \(\Delta ABC = \Delta DEF\left( {c - g - c} \right)\)
b)
-Chứng minh \(HB = KE;HC = KF \Rightarrow BC = EF\)
Lời giải chi tiết:
a)
Xét \(\Delta HAB\) và \(\Delta KDE\) có:
\(\widehat H = \widehat K = {90^0}\\HA = KD\left( {gt} \right)\\AB = DE\left( {gt} \right)\\ \Rightarrow \Delta HAB = \Delta KDE\left( {ch - cgv} \right)\)
\(\Rightarrow \widehat {ABH} = \widehat {DEK}\) ( 2 góc tương ứng) hay \(\widehat {ABC} = \widehat {DEF}\)
Xét \(\Delta ABC\) và \(\Delta DEF\) có:
\(\begin{array}{l}BA = ED\\BC = EF\\\widehat {ABC} = \widehat {DEF}\\ \Rightarrow \Delta ABC = \Delta DEF\left( {c - g - c} \right)\end{array}\)
b)
Chứng minh tương tự như trên có các cặp tam giác vuông bằng nhau:
\(\Delta HAB = \Delta KDE;\Delta HAC = \Delta KDF\)
\( \Rightarrow HB = KE;HC = KF\) (cặp cạnh tương ứng)
Ta có:
\(\left\{ \begin{array}{l}BC = HB + HC\\EF = KE + KF\end{array} \right. \Rightarrow BC = EF\)
Xét \(\Delta ABC\) và \(\Delta DEF\) có:
\(\begin{array}{l}AB = DE\left( {gt} \right)\\AC = DF\left( {gt} \right)\\BC = EF\left( {cmt} \right)\\ \Rightarrow \Delta ABC = \Delta DEF\left( {c - c - c} \right)\end{array}\)
-- Mod Toán 7 HỌC247
Bài tập SGK khác
Giải bài 4.35 trang 65 SBT Toán 7 Kết nối tri thức tập 1 - KNTT
Giải bài 4.36 trang 65 SBT Toán 7 Kết nối tri thức tập 1 - KNTT
Giải bài 4.38 trang 66 SBT Toán 7 Kết nối tri thức tập 1 - KNTT
Giải bài 4.39 trang 66 SBT Toán 7 Kết nối tri thức tập 1 - KNTT
Giải bài 4.40 trang 66 SBT Toán 7 Kết nối tri thức tập 1 - KNTT
Chưa có câu hỏi nào. Em hãy trở thành người đầu tiên đặt câu hỏi.


