Giải bài 65 tr 49 sách BT Toán lớp 7 Tập 2
Cho hình 13. Chứng minh rằng ba điểm \(B, K, C\) thẳng hàng.
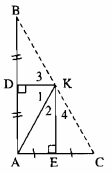
Hướng dẫn giải chi tiết
Hướng dẫn giải
Sử dụng:
+) Điểm nằm trên đường trung trực của một đoạn thẳng thì cách đều hai mút của đoạn thẳng đó
+) Tính chất tam giác cân
Lời giải chi tiết
Nối KA, KB, KC.
Ta có KD là đường trung trực của AB
\( \Rightarrow \) KA = KB (tính chất đường trung trực)
\( \Rightarrow \) ∆KAB cân tại K nên KD là đường phân giác của \(\widehat {AKB}\)
\( \Rightarrow \) \(\widehat {{K_1}} = \widehat {{K_3}}\)
\( \Rightarrow \) \(\widehat {AKB} = 2\widehat {{K_1}}\) (1)
KE là đường trung trực của AC
\( \Rightarrow \) KA = KC (tính chất đường trung trực)
\( \Rightarrow \) ∆KAC cân tại K nên KE là đường phân giác của \(\widehat {AKC}\)
\( \Rightarrow \) \(\widehat {{K_2}} = \widehat {{K_4}}\)
\( \Rightarrow \widehat {AKC} = 2\widehat {{K_2}}\left( 2 \right)\)
\(\eqalign{
& K{\rm{D}} \bot AB\left( {gt} \right) \cr
& AC \bot AB\left( {gt} \right) \cr} \)
-- Mod Toán 7 HỌC247
Bài tập SGK khác
-


Cho tam giác ABC (AB>AC).>Trên tia đối tia AB lấy điểm E,trên tia đối tia AC lấy điểm D,sao cho AB=AD và AC=AE.các tia DE và BC cắt nhau tại I
C/m tam giác ABC= tam giác ADE
b Góc ACI= góc AEI
IB=ID
Theo dõi (0) 1 Trả lời -


Chứng minh DE song song AH biết AH vuông góc BC
bởi Quỳnh Giao
 21/12/2019
21/12/2019
cho tam giác ABC vuông tại A, vẽ tia phân giác của góc ABC cắt cạnh AC tại D. trên cạnh BC lấy điểm E sao cho BE=BA
a) Chứng minh tam giác ABD = tam giác EBD
b) vẽ AH vuông góc BC (H thuộc BC), chứng minh DE song song AH
c) chứng minh AE là tia phân giác của góc HAD
Theo dõi (1) 1 Trả lời -


Chứng minh HA=HB biết Ot là tia phân giác của góc xOy
bởi Mạc Tử Hàn
 20/12/2019
20/12/2019
Cho goc XOY ,gọi OT là tia phân giác của góc đó .Trên tia Ox lấy điểm A ,trên tia oy lấy điểm B, sao cho OA=OB
tia Ot cắt AB tại H
C/m HA=HB
C/m ot là đường trung trực của AB
Lấy điểm M thuộc tia Ax ,từ M kẻ Mn //AB (n thuộc 0y)
C/m AM=BN
Theo dõi (0) 4 Trả lời -


Cho ∆ ABC, E là trung điểm của BC. Lấy D thuộc tia đối của tia EA sao cho ED = EA.
a)Chứng minh rằng: ∆AEB = ∆DEC
b) Chứng minh rằng: AC // BD
Theo dõi (0) 2 Trả lời -
ADMICRO


Cho tam giác ABC có AB bé hơn AC .Trên tia đối của tia CA lấy điểm D sao cho CD=AB. Gọi P,Q là trung điểm của AD và BC và I là giao điểm của các đường vuông góc với AD và BC tại P và Q a) CMR: Tam giác AIB= tam giác DIC b)CM AI là tia phân giác của góc BAC c) Kẻ IE vuông góc với AB ,chứng minh 2AE= AD
Theo dõi (0) 2 Trả lời -


Câu 8. (2,0 điểm) Cho góc xOy bằng 60°. Tia Oz là phân giác của góc xOy. Từ điểm B bất kì trên tia Ox kẻ BH, BK lần lượt vuông góc với Oy, Oz tại H và K. Qua B kẻ đường song song với Oy cắt Oz tại M. Chứng minh rằng BH=MK.
Câu 9. (2,0 điểm) Cho tam giác ABC vuông cân tại A. Điểm M nằm bên trong tam giác sao cho MA=2cm, MB=3cm và AMC =135°. Tính MC.
Câu 10. (2,0 điểm) Từ 200 số tự nhiên 1; 2; 3,...; 200, ta lấy ra k số bất ki sao cho trong các số vừa lấy luôn tìm được 2 số mà số này là bội của số kia. Tìm giá trị nhỏ nhất của k.
Theo dõi (0) 0 Trả lời -


Có góc B bằng góc C Kẻ AH vuông góc với BC H thuộc BC trên tia đối của tia bc lấy điểm D trên tia đối của tia CB lấy điểm E sao cho BD = CE, kẻ BD vuông góc với AD vuông góc với AE Chứng minh ba đường thẳng AH, BK,CI cùng đi qua một điểm
Theo dõi (0) 1 Trả lời -


Cho hình chóp tứ giác S.ABCD có đáy là hình chữ nhật cạnh A B = a , A D = a căn 2
bởi Lý Chí Phàm
 12/12/2019
Cho hình chóp tứ giác S.ABCD có đáy là hình chữ nhật cạnh A B = a , A D = a √ 2 , S A ⊥ ( A B C D ) góc giữa SC và đáy bằng 60 độ. Tính thể tích hình chóp S.ABCD.Theo dõi (0) 0 Trả lời
12/12/2019
Cho hình chóp tứ giác S.ABCD có đáy là hình chữ nhật cạnh A B = a , A D = a √ 2 , S A ⊥ ( A B C D ) góc giữa SC và đáy bằng 60 độ. Tính thể tích hình chóp S.ABCD.Theo dõi (0) 0 Trả lời -


Tam giác ABC có góc A1: B1: C1 là các ngoài tỉ lệ nghịch với 1/4: 1/5: 1/6
bởi Huyền Trang
 30/11/2019
30/11/2019
Tam giác ABC có góc A1: B1: C1 là các ngoài tỉ lệ nghịch với 1/4: 1/5: 1/6. Hỏi các góc trong A2; B2;C2 tỉ lệ với các số nào
Theo dõi (0) 0 Trả lời -


Chứng minh hai tam giác bằng nhau
bởi Hien Trinh
 29/11/2019
Cau 6
29/11/2019
Cau 6 Theo dõi (1) 2 Trả lời
Theo dõi (1) 2 Trả lời -


cho tam giác ABC biết A=90 độ B=60 độ vậy C=?
Theo dõi (0) 18 Trả lời -


Cho tam giác ABC, góc a bằng 90 độ,gọi M là trung điểm của BC.Trên tia đối của tia MA lấy điểm E sao cho ME bằng MA
a, cm tam giác AMB bằng tam giác EMC
b,tính góc ACE
c,cm BE // AC
Theo dõi (0) 2 Trả lời -


Tính độ dài mỗi cạnh của một tam giác biết chu vi là 72 cm và ba cạnh của tam giác này lần lượt tỉ lệ với 3, 4, 5
bởi Lương Hồng Phát
 27/11/2019
Hãy giúp tôiTheo dõi (3) 10 Trả lời
27/11/2019
Hãy giúp tôiTheo dõi (3) 10 Trả lời -


Cho góc xAy= 90 độ. Điểm C thuộc tia phân giác của góc xAy. Từ C, kẻ CD vuông góc với Ax tại D, CB vuông góc với Ax tại B. Trên các đoạn thẳng AD và AB, lấy điểm P,Q sao cho chu vi tam giác APQ=AD+AB.Điểm E thuộc tia Dx sao cho DE=QB.
A) CMR: PC là tia phân giác của góc DPQ
B) CMR góc PCQ=45 độ
Theo dõi (1) 5 Trả lời -


Cho tam giác ABC vuông tại A;AB
bởi Kim Taehoon
 17/11/2019
17/11/2019
Cho tam giác ABC vuông tại A;AB<AC.Trên tia đối của tia AC lấy điểm M sao cho A là trung điểm MC.
a)Chứng minh:tam giác ABC=tam giác ABM
b)Trên tia BA lấy điểm I sao cho A là trung điểm của BI.Chứng minh cho BC//IM.
Chỉ cần vẽ hình thôi còn lại mình tự làm
Theo dõi (0) 2 Trả lời -


Cho tam giác ABC có AB = AC. Gọi M là trung điểm của BC
bởi Sen Pai
 11/11/2019
11/11/2019
cho tam giác ABC có AB = AC. Gọi M là trung điểm của BC
a) Chứng minh: Tam giác AMB = Tam giác AMC
b) Chứng minh: AM là phân giác của góc BAC
c) Chứng minh: AM vuông góc với BC
d) Trên nửa mặt phẳng bờ BC không chứa điểm A, lấy điểm D sao cho DB = DC. Chứng minh 3 điểm A, M, D thẳng hàng
Theo dõi (1) 3 Trả lời -


Tính các góc của tam giác trong các trường hợp tam giác đó có ba góc trong bằng nhau
bởi Edogawa Conan
 10/11/2019
10/11/2019
Tính các góc của một tam giác trong các trường hợp sau:
a) tam giác đó có ba góc trong bằng nhau.
b) Tam giác đó có hai góc trong bằng nhau, còn góc kia bằng 40 độ.
Theo dõi (1) 5 Trả lời -


Lập sơ đồ lý thuyết tính chất dãy tỉ số bằng nhau và sơ đồ tóm tắt về tỉ lệ thức,số vô tỉ,số thực,căn bậc hai.
bởi Vũ Minh Anh
 29/10/2019
29/10/2019
Lập sơ đồ lý thuyết tính chất dãy tỉ số bằng nhau và sơ đồ tóm tắt về tỉ lệ thức,số vô tỉ,số thực,căn bậc hai.
Theo dõi (0) 0 Trả lời -


cho goc xoy tren ox va oy lan luot lay hai diem a va b sao cho oa =ob tia phan giac oz cua xoy cat ab tai c . a cm c la trung diem cua ab va ab vuong goc voi oc . b tren oz lay m sao cho oc=om cmr am song song ob bm song song oa . c ke mi vuong goc voi oy mk vuong goc voi õ so sanh bi va ak . d goi n la giao diem cua ai va bk cmr o,n,m thang hang
Theo dõi (0) 7 Trả lời -


cho tam giác ABC vuông tại B và phân giác AD . Gọi E là hình chiếu của D trên AC , tia ED cắt tia AB tại F . CMR
a) tam giác BDF = tam giác EDC
b) AD là trung trực của đoạn thẳng FC
c) tam giác ABC có thêm điều kiện gì để D là trọng tâm của tam giác AFC
Theo dõi (0) 5 Trả lời







