Toán 7 Chân trời sáng tạo Bài 3: Hai đường thẳng song song

Ví dụ:

a) Trong Hình 4a, hai đường thẳng m và n song song vì chúng tạo với đường thẳng d hai góc đồng vị bằng nhau.

b) Trong Hình 4b, hai đường thẳng e và d song song vì chủng tạo với đường thẳng h hai góc so le trong băng nhau.

Chú ý: Hai đường thẳng phân biệt cùng vuông góc với một đường thẳng thứ ba thì chúng song song với nhau.

Cách vẽ hai đường thẳng song song

Vận dụng tính chất vừa học ta có thể vẽ hai đường thẳng song song a và b bằng nhiều cách, chăng hạn như:

- Vẽ a, b cùng vuông góc với một đường thẳng d (Hình 7a)

- Vẽ a, b cùng tạo với đường thẳng d những góc so le trong hoặc đồng vị bằng nhau (Hình 7b).

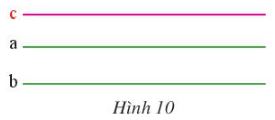
Ví dụ: Cho hai đường thẳng phân biệt a và b cùng song song với đường thẳng c (Hình 10) Hãy giải thích tại sao a // b.

Giải

Ta có a // e và b // c (a khác b). Nếu a có điểm chung M với b thì qua điểm M ta vẽ được hai đường thẳng là a và b cùng song song với c, điều này trải với tiên đề Euclid.

Vậy a không có điểm chung với b, suy ra a//b

Chú ý: Hai đường thẳng phân biệt cùng song song với một đường thẳng thứ ba thì song song với nhau. 

Ví dụ: Trong Hình 11, đường thẳng c cắt hai đường thẳng song song a và b lần lượt tại A và B nên ta có:

a) \(\widehat {{A_3}} = \widehat {{B_1}},\widehat {{A_4}} = \widehat {{B_2}}\) (các cặp góc so le trong)

b) \(\widehat {{A_1}} = \widehat {{B_1}},\widehat {{A_3}} = \widehat {{B_3}}\) (các cặp góc đồng vị)

Chú ý: Một đường thẳng vuông góc với một trong hai đường thẳng song song thì nó cũng vuông góc với đường thẳng còn lại.

Câu 1: Tìm các cặp đường thẳng song song trong Hình sau và giải thích.

Hướng dẫn giải

Xét hình a: a // b vì đường thẳng c cắt 2 đường thẳng a, b và tạo thành một cặp góc so le trong bằng nhau

Xét hình b: không có cặp đường thẳng nào song song vì đường thẳng g cắt 2 đường thẳng d, e và không tạo thành một cặp góc so le trong bằng nhau ( 90 \(^\circ \) khác 80 \(^\circ \))

Xét hình c: m // n vì đường thẳng p cắt 2 đường thẳng m, n và tạo thành một cặp góc đồng vị bằng nhau

Câu 2:

a) Cho tam giác ABC. Hãy nêu cách vẽ đường thẳng a đi qua A và song song với BC, vẽ đường thẳng b đi qua B và song song với AC.

b) Có thể vẽ được bao nhiêu đường thẳng a, bao nhiêu đường thẳng b? Vì sao?

Hướng dẫn giải

+ Vẽ đường thẳng a đi qua A sao cho a và BC tạo với đường thẳng AB cặp góc so le trong bằng nhau.

+ Vẽ đường thẳng b đi qua B sao cho b và AC tạo với đường thẳng BC cặp góc so le trong bằng nhau.

Lời giải chi tiết:

Đo góc ABC. Vẽ đường thẳng a đi qua A sao cho góc tạo bởi a và đường thẳng AB bằng góc ABC.

Ta được đường thẳng a đi qua A và song song với BC

Đo góc ACB. Vẽ đường thẳng b đi qua B sao cho góc tạo bởi b và đường thẳng BC bằng góc ACB.

Ta được đường thẳng b đi qua B và song song với AC

b) Có thể vẽ được chỉ 1 đường thẳng a, 1 đường thẳng b thoả mãn yêu cầu. Vì qua 1 điểm nằm ngoài  một đường thẳng, chỉ có 1 đường thẳng song song với nó

Qua bài giảng ở trên, giúp các em học sinh:

- Mô tả được dấu hiệu song song của hai đường thẳng thông qua cặp góc đồng vị, cặp góc so le trong.

- Nhận biết được tiên đề Euclid về đường thẳng song song.

- Mô tả được một số tính chất của hai đường thẳng song song.

Để củng cố bài học xin mời các em cùng làm Bài kiểm tra Trắc nghiệm Toán 7 Chân trời sáng tạo Chương 4 Bài 3 để kiểm tra xem mình đã nắm được nội dung bài học hay chưa.

• Câu 1:

  Cho hình vẽ sau:

  
  

  Khẳng định nào sau đây là sai?

  • A.  yy' // zz^'
  • B.  \(\widehat {ADt'} = {125^0}\)
  • C.  \(\widehat {CDz'} = {135^0}\)
  • D.  \(\widehat {ADC} = {55^0}\)

• Câu 2:

  Cho hình vẽ, biết AB // CD. Tính góc A, góc B

  

  • A.  \(\widehat A = {115^0};\widehat B = {130^0}\)
  • B.  \(\widehat A = {110^0};\widehat B = {130^0}\)
  • C.  \(\widehat A = {115^0};\widehat B = {150^0}\)
  • D.  \(\widehat A = {135^0};\widehat B = {110^0}\)

• Câu 3:

  Cho hình vẽ sau, biết x // y và \( \widehat {{M_1}} = {55^0}.\). Tính số đo góc \(\widehat {{N_1}}\)

  

  • A. 55⁰
  • B. 35⁰
  • C. 60⁰
  • D. 125⁰

Câu 4-10: Mời các em đăng nhập xem tiếp nội dung và thi thử Online để củng cố kiến thức và nắm vững hơn về bài học này nhé!

Bên cạnh đó các em có thể xem phần hướng dẫn Giải bài tập Toán 7 Chân trời sáng tạo Chương 4 Bài 3 để giúp các em nắm vững bài học và các phương pháp giải bài tập.

Câu hỏi mở đầu trang 76 SGK Toán 7 Chân trời sáng tạo tập 1 - CTST

Hoạt động khám phá 1 trang 76 SGK Toán 7 Chân trời sáng tạo tập 1 - CTST

Thực hành 1 trang 77 SGK Toán 7 Chân trời sáng tạo tập 1 - CTST

Thực hành 2 trang 77 SGK Toán 7 Chân trời sáng tạo tập 1 - CTST

Hoạt động khám phá 2 trang 78 SGK Toán 7 Chân trời sáng tạo tập 1 - CTST

Thực hành 3 trang 79 SGK Toán 7 Chân trời sáng tạo tập 1 - CTST

Hoạt động khám phá 3 trang 79 SGK Toán 7 Chân trời sáng tạo tập 1 - CTST

Thực hành 3 trang 79 SGK Toán 7 Chân trời sáng tạo tập 1 - CTST

Vận dụng 1 trang 80 SGK Toán 7 Chân trời sáng tạo tập 1 - CTST

Vận dụng 2 trang 80 SGK Toán 7 Chân trời sáng tạo tập 1 - CTST

Giải bài 1 trang 80 SGK Toán 7 Chân trời sáng tạo tập 1 - CTST

Giải bài 2 trang 80 SGK Toán 7 Chân trời sáng tạo tập 1 - CTST

Giải bài 3 trang 80 SGK Toán 7 Chân trời sáng tạo tập 1 - CTST

Giải bài 4 trang 80 SGK Toán 7 Chân trời sáng tạo tập 1 - CTST

Giải bài 5 trang 80 SGK Toán 7 Chân trời sáng tạo tập 1 - CTST

Giải bài 6 trang 81 SGK Toán 7 Chân trời sáng tạo tập 1 - CTST

Giải bài 7 trang 81 SGK Toán 7 Chân trời sáng tạo tập 1 - CTST

Giải bài 1 trang 83 SBT Toán 7 Chân trời sáng tạo tập 1 - CTST

Giải bài 2 trang 83 SBT Toán 7 Chân trời sáng tạo tập 1 - CTST

Giải bài 3 trang 83 SBT Toán 7 Chân trời sáng tạo tập 1 - CTST

Giải bài 4 trang 83 SBT Toán 7 Chân trời sáng tạo tập 1 - CTST

Giải bài 5 trang 83 SBT Toán 7 Chân trời sáng tạo tập 1 - CTST

Trong quá trình học tập nếu có thắc mắc hay cần trợ giúp gì thì các em hãy comment ở mục Hỏi đáp, Cộng đồng Toán HOC247 sẽ hỗ trợ cho các em một cách nhanh chóng!

Chúc các em học tập tốt và luôn đạt thành tích cao trong học tập!