Nếu các em gặp khó khăn hay có những bài toán hay muốn chia sẻ trong quá trình làm bài tập liên quan đến Ứng dụng tích phân tính diện tích hình phẳng và thể tích khối tròn xoay từ bài tập SGK, Sách tham khảo, Các trang mạng cộng đồng Toán HỌC247 sẽ sớm giải đáp cho các em.
Danh sách hỏi đáp (161 câu):
-
Tính diện tích hình phẳng giới hạn bởi: Đồ thị hai hàm số \(y = {x^2}\) và \(y = - {x^2} - 2x\)
07/05/2021 | 1 Trả lời
Tính diện tích hình phẳng giới hạn bởi: Đồ thị hai hàm số \(y = {x^2}\) và \(y = - {x^2} - 2x\)
Theo dõi (0)Gửi câu trả lời Hủy -
Tính diện tích hình phẳng giới hạn bởi: Đồ thị các hàm số \(y = {x^2} - 4\), \(y = - {x^2} - 2x\) và đường thẳng \(x = - 3,x = - 2;\)
07/05/2021 | 1 Trả lời
Tính diện tích hình phẳng giới hạn bởi: Đồ thị các hàm số \(y = {x^2} - 4\), \(y = - {x^2} - 2x\) và đường thẳng \(x = - 3,x = - 2;\)
Theo dõi (0)Gửi câu trả lời Hủy -
Hãy tính diện tích hình phẳng giới hạn bởi: Đồ thị hàm số \(y = 2{x^2}\) và \(y = {x^4} - 2{x^2}\) trong miền \(x \ge 0.\)
07/05/2021 | 1 Trả lời
Hãy tính diện tích hình phẳng giới hạn bởi: Đồ thị hàm số \(y = 2{x^2}\) và \(y = {x^4} - 2{x^2}\) trong miền \(x \ge 0.\)
Theo dõi (0)Gửi câu trả lời Hủy -
Hãy tính diện tích hình phẳng giới hạn bởi: Đồ thị hai hàm số \(y = \sqrt x \) và \(y = \root 3 \of x \).
07/05/2021 | 1 Trả lời
Hãy tính diện tích hình phẳng giới hạn bởi: Đồ thị hai hàm số \(y = \sqrt x \) và \(y = \root 3 \of x \).
Theo dõi (0)Gửi câu trả lời Hủy -

Hãy tính diện tích hình phẳng giới hạn bởi: Đồ thị hàm số \(y = {\cos ^2}x,\) trục hoành, trục tung và đường thẳng \(x = \pi \).
07/05/2021 | 1 Trả lời
Hãy tính diện tích hình phẳng giới hạn bởi: Đồ thị hàm số \(y = {\cos ^2}x,\) trục hoành, trục tung và đường thẳng \(x = \pi \).
Theo dõi (0)Gửi câu trả lời Hủy -
Hãy tính diện tích hình phẳng giới hạn bởi đồ thị hàm số \(y = {\mathop{\rm s}\nolimits} {\rm{inx}} + 1\), trục hoành và hai đường thẳng \(x=0\) và \(x = {{7\pi } \over 6}\)
07/05/2021 | 1 Trả lời
Hãy tính diện tích hình phẳng giới hạn bởi đồ thị hàm số \(y = {\mathop{\rm s}\nolimits} {\rm{inx}} + 1\), trục hoành và hai đường thẳng \(x=0\) và \(x = {{7\pi } \over 6}\)
Theo dõi (0)Gửi câu trả lời Hủy -
Hãy tính thể tích khối tròn xoay do hình phẳng giới hạn bởi các đường sau quay quanh trục \(Ox\): \(y = \tan x, y = 0, x = 0\), \(x=\dfrac{\pi }{4}\).
05/05/2021 | 1 Trả lời
Hãy tính thể tích khối tròn xoay do hình phẳng giới hạn bởi các đường sau quay quanh trục \(Ox\): \(y = \tan x, y = 0, x = 0\), \(x=\dfrac{\pi }{4}\).
Theo dõi (0)Gửi câu trả lời Hủy -
Hãy tính thể tích khối tròn xoay do hình phẳng giới hạn bởi các đường sau quay quanh trục \(Ox\): \(y = \cos x, y = 0, x = 0, x = π\).
05/05/2021 | 1 Trả lời
Hãy tính thể tích khối tròn xoay do hình phẳng giới hạn bởi các đường sau quay quanh trục \(Ox\): \(y = \cos x, y = 0, x = 0, x = π\).
Theo dõi (0)Gửi câu trả lời Hủy -
Hãy tính thể tích khối tròn xoay do hình phẳng giới hạn bởi các đường sau quay quanh trục \(Ox\): \(y = 1 - x^2\), \(y = 0\).
05/05/2021 | 1 Trả lời
Hãy tính thể tích khối tròn xoay do hình phẳng giới hạn bởi các đường sau quay quanh trục \(Ox\): \(y = 1 - x^2\), \(y = 0\).
Theo dõi (0)Gửi câu trả lời Hủy -
Cho Parabol \(y = {{{x^2}} \over 2}\) chia hình tròn có tâm tại gốc tọa độ, bán kính \(2\sqrt2\) thành hai phần. Tìm tỉ số diện tích của chúng.
05/05/2021 | 1 Trả lời
Cho Parabol \(y = {{{x^2}} \over 2}\) chia hình tròn có tâm tại gốc tọa độ, bán kính \(2\sqrt2\) thành hai phần. Tìm tỉ số diện tích của chúng.
Theo dõi (0)Gửi câu trả lời Hủy -
Hãy tính diện tích hình phẳng giới hạn bởi đường cong \(y = {x^2} + 1\), tiếp tuyến với đường này tại điểm \(M(2;5)\) và trục \(Oy\).
06/05/2021 | 1 Trả lời
Hãy tính diện tích hình phẳng giới hạn bởi đường cong \(y = {x^2} + 1\), tiếp tuyến với đường này tại điểm \(M(2;5)\) và trục \(Oy\).
Theo dõi (0)Gửi câu trả lời Hủy -
Hãy tính diện tích hình phẳng giới hạn bởi các đường: \(y = {\left( x-6 \right)}^2,y = 6x-{x^2}\).
06/05/2021 | 1 Trả lời
Hãy tính diện tích hình phẳng giới hạn bởi các đường: \(y = {\left( x-6 \right)}^2,y = 6x-{x^2}\).
Theo dõi (0)Gửi câu trả lời Hủy -
Hãy tính diện tích hình phẳng giới hạn bởi các đường: \(y={x^2},y =x + 2\).
Theo dõi (0)Gửi câu trả lời Hủy -
Khái niệm mặt tròn xoay và khối tròn xoay trong hình học là gì?
Theo dõi (0)Gửi câu trả lời Hủy -
Hãy tính diện tích hình thang vuông được giới hạn các đường thẳng: \(y = -2x – 1, y = 0, x = 1\) và \(x = 5\).
06/05/2021 | 1 Trả lời
Hãy tính diện tích hình thang vuông được giới hạn các đường thẳng: \(y = -2x – 1, y = 0, x = 1\) và \(x = 5\).
Theo dõi (0)Gửi câu trả lời Hủy -
 Theo dõi (0)Gửi câu trả lời Hủy
Theo dõi (0)Gửi câu trả lời Hủy -
 Theo dõi (0)Gửi câu trả lời Hủy
Theo dõi (0)Gửi câu trả lời Hủy -
UvucgcuvucigivfTheo dõi (0)Gửi câu trả lời Hủy
-
Tính diện tích hình phẳng giới hạn bởi các đường y = x 2 , y 4x 2 , y=4Theo dõi (1)Gửi câu trả lời Hủy
-
Tính diện tích hình phẳng giới hạn bởi đồ thị hàm số \(y = 4 - x^2\) và trục hoành?
31/07/2020 | 1 Trả lời
Diện tích hình phẳng giới hạn không gian bởi đồ thị hàm số y=4x-x^2 và trục hoành bằng
Theo dõi (0)Gửi câu trả lời Hủy -
Diện tích hình phẳng?
17/06/2020 | 3 Trả lời
Diện tích hình phẳng giới hạn bởi các đường
y=(x-1)ex , y=1-x,x=0 được xác định bởi công thức nào?
Theo dõi (1)Gửi câu trả lời Hủy -
Diện tích hình phẳng giới hạn bởi các đường y=2x-1 , y=6:x , x=3 là :Theo dõi (0)Gửi câu trả lời Hủy
-
Diện tích mặt phẳng giới hạn bởi đường thẳng y=2x +1và đồ thị hàm số y=x^2-x+ 3
02/06/2020 | 1 Trả lời
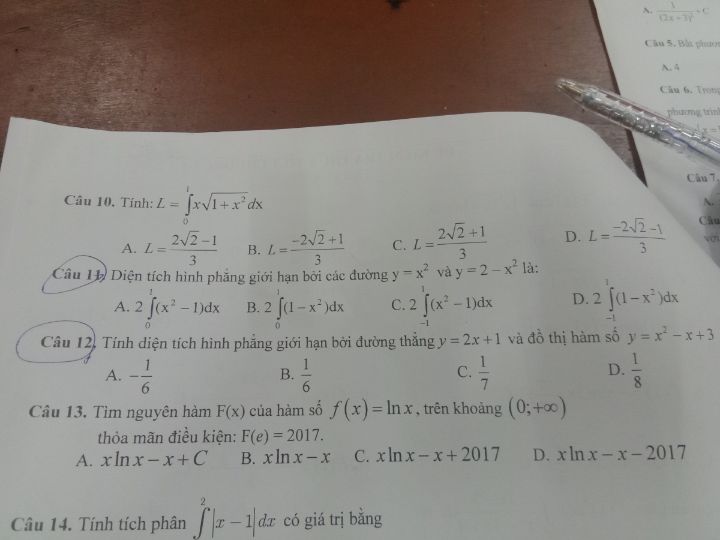 Theo dõi (0)Gửi câu trả lời Hủy
Theo dõi (0)Gửi câu trả lời Hủy -
Cho hàm số f(x) có đạo hàm trên đoạn [1;2], f(1) = 1 và f(2) = 2. Tính \(I = \int\limits_1^2 {f'\left( x \right){\rm{d}}x} \)
30/05/2020 | 1 Trả lời
Theo dõi (0)Gửi câu trả lời Hủy -
Công thức tính thể tích V của khối tròn xoay được tạo ra khi quay hình thang cong, giới hạn bởi đồ thị hàm số y = f(x), trục Ox và hai đường thẳng x = 1, x = b (a < b), xung quanh trục Ox.
31/05/2020 | 1 Trả lời
A. \(V = \pi \int\limits_a^b {{f^2}\left( x \right){\rm{d}}x} \) .
B. \(V = \int\limits_a^b {{f^2}\left( x \right){\rm{d}}x} \) .
C. \(V = \pi \int\limits_a^b {f\left( x \right){\rm{d}}x} \) .
D. \(V = \int\limits_a^b {\left| {f\left( x \right)} \right|{\rm{d}}x} \) .
Theo dõi (0)Gửi câu trả lời Hủy


