Nß║┐u c├íc em gß║Àp kh├│ kh─ân hay c├│ nhß╗»ng b├ái to├ín hay muß╗æn chia sß║╗ trong qu├í tr├¼nh l├ám b├ái tß║¡p li├¬n quan ─æß║┐n t├¼m T├¡ch ph├ón tß╗½ b├ái tß║¡p SGK, S├ích tham khß║úo, C├íc trang mß║íng cß╗Öng ─æß╗ông To├ín Hß╗îC247 sß║¢ sß╗øm giß║úi ─æ├íp cho c├íc em.
Danh sách hỏi đáp (598 câu):
-
Hãy tính \(\int\limits_0^{{\pi \over 2}} {{{dx} \over {2 + c{\rm{os}}x}}} \)
25/05/2021 | 1 Trß║ú lß╗Øi
Hãy tính \(\int\limits_0^{{\pi \over 2}} {{{dx} \over {2 + c{\rm{os}}x}}} \)
Theo d├Ái (0)Gß╗¡i c├óu trß║ú lß╗Øi Hß╗ºy -
Cho a > 0. Chß╗®ng minh rß║▒ng|: \(\int\limits_\alpha ^\beta {{{dx} \over {{x^2} + {a^2}}} = {1 \over a}\left( {r - k} \right)} \) trong ─æ├│ r v├á k l├á c├íc sß╗æ thß╗▒c thß╗Åa m├ún \({\rm{tan}}r = {\beta \over a},\tan k = {\alpha \over a}\)
24/05/2021 | 1 Trß║ú lß╗Øi
Cho a > 0. Chß╗®ng minh rß║▒ng: \(\int\limits_\alpha ^\beta {{{dx} \over {{x^2} + {a^2}}} = {1 \over a}\left( {r - k} \right)} \) trong ─æ├│ r v├á k l├á c├íc sß╗æ thß╗▒c thß╗Åa m├ún \({\rm{tan}}r = {\beta \over a},\tan k = {\alpha \over a}\).
Theo d├Ái (0)Gß╗¡i c├óu trß║ú lß╗Øi Hß╗ºy -
Tính tích phân sau: \(\int\limits_0^{{\pi \over 2}} {{1 \over {1 + c{\rm{os}}x}}dx} \).
25/05/2021 | 1 Trß║ú lß╗Øi
Tính tích phân sau: \(\int\limits_0^{{\pi \over 2}} {{1 \over {1 + c{\rm{os}}x}}dx} \).
Theo d├Ái (0)Gß╗¡i c├óu trß║ú lß╗Øi Hß╗ºy -
Tính tích phân sau: \(\int\limits_1^2 {x\sqrt {{x^2} + 3} dx} \)
Theo d├Ái (0)Gß╗¡i c├óu trß║ú lß╗Øi Hß╗ºy -

Tính tích phân sau: \(\int\limits_0^{{\pi \over {12}}} {{1 \over {{\rm{co}}{{\rm{s}}^2}3x\left( {1 + \tan 3x} \right)}}dx} \).
24/05/2021 | 1 Trß║ú lß╗Øi
Tính tích phân sau: \(\int\limits_0^{{\pi \over {12}}} {{1 \over {{\rm{co}}{{\rm{s}}^2}3x\left( {1 + \tan 3x} \right)}}dx} \).
Theo d├Ái (0)Gß╗¡i c├óu trß║ú lß╗Øi Hß╗ºy -
Tính tích phân sau: \(\int\limits_0^{{\pi \over 2}} {{{{\rm{cos}}x} \over {1 + \sin x}}dx} \).
24/05/2021 | 1 Trß║ú lß╗Øi
Tính tích phân sau: \(\int\limits_0^{{\pi \over 2}} {{{{\rm{cos}}x} \over {1 + \sin x}}dx} \).
Theo d├Ái (0)Gß╗¡i c├óu trß║ú lß╗Øi Hß╗ºy -
Tính tích phân sau: \(\int\limits_{10}^{12} {{{2x + 1} \over {{x^2} + x - 2}}dx} \).
24/05/2021 | 1 Trß║ú lß╗Øi
Tính tích phân sau: \(\int\limits_{10}^{12} {{{2x + 1} \over {{x^2} + x - 2}}dx} \).
Theo d├Ái (0)Gß╗¡i c├óu trß║ú lß╗Øi Hß╗ºy -
Tính tích phân sau: \(\int\limits_0^1 {{{2{x^2}} \over {{x^3} + 1}}dx} \).
24/05/2021 | 1 Trß║ú lß╗Øi
Tính tích phân sau: \(\int\limits_0^1 {{{2{x^2}} \over {{x^3} + 1}}dx} \).
Theo d├Ái (0)Gß╗¡i c├óu trß║ú lß╗Øi Hß╗ºy -
Tính tích phân sau: \(\int\limits_1^1 {{{2x} \over {{x^2} + 1}}dx} \).
24/05/2021 | 1 Trß║ú lß╗Øi
Tính tích phân sau: \(\int\limits_1^1 {{{2x} \over {{x^2} + 1}}dx} \).
Theo d├Ái (0)Gß╗¡i c├óu trß║ú lß╗Øi Hß╗ºy -
Tính tích phân sau: \(\int\limits_1^2 {{3 \over {1 - 2x}}dx} \).
Theo d├Ái (0)Gß╗¡i c├óu trß║ú lß╗Øi Hß╗ºy -
Tính tích phân sau: \(\int\limits_4^5 {{{\left( {{x^2} + {1 \over x}} \right)}^2}dx} \).
24/05/2021 | 1 Trß║ú lß╗Øi
Tính tích phân sau: \(\int\limits_4^5 {{{\left( {{x^2} + {1 \over x}} \right)}^2}dx} \).
Theo d├Ái (0)Gß╗¡i c├óu trß║ú lß╗Øi Hß╗ºy -
Tính tích phân sau: \(\int\limits_0^{16} {{{dx} \over {\sqrt {x + 9} - \sqrt x }}} \).
25/05/2021 | 1 Trß║ú lß╗Øi
Tính tích phân sau: \(\int\limits_0^{16} {{{dx} \over {\sqrt {x + 9} - \sqrt x }}} \).
Theo d├Ái (0)Gß╗¡i c├óu trß║ú lß╗Øi Hß╗ºy -
Tính tích phân sau: \(\int\limits_0^2 {\left| {1 - x} \right|dx} \)
Theo d├Ái (0)Gß╗¡i c├óu trß║ú lß╗Øi Hß╗ºy -
Tính tích phân sau: \(\int\limits_0^\pi {\left| {{\rm{cos}}x} \right|dx} \).
25/05/2021 | 1 Trß║ú lß╗Øi
Tính tích phân sau: \(\int\limits_0^\pi {\left| {{\rm{cos}}x} \right|dx} \).
Theo d├Ái (0)Gß╗¡i c├óu trß║ú lß╗Øi Hß╗ºy -
Mß╗Öt vß║¡t chuyß╗ân ─æß╗Öng vß╗øi vß║¡n tß╗æc \(v\left( t \right) = 1,2 + {{{t^2} + 4} \over {t + 3}}\left( {m/s} \right)\). T├¡nh qu├úng ─æã░ß╗Øng vß║¡t ─æ├│ ─æi ─æã░ß╗úc tr├▓n 4 gi├óy (l├ám tr├▓n kß║┐t quß║ú ─æß║┐n h├áng phß║ºn tr─âm)
24/05/2021 | 1 Trß║ú lß╗Øi
Mß╗Öt vß║¡t chuyß╗ân ─æß╗Öng vß╗øi vß║¡n tß╗æc \(v\left( t \right) = 1,2 + {{{t^2} + 4} \over {t + 3}}\left( {m/s} \right)\). T├¡nh qu├úng ─æã░ß╗Øng vß║¡t ─æ├│ ─æi ─æã░ß╗úc tr├▓n 4 gi├óy (l├ám tr├▓n kß║┐t quß║ú ─æß║┐n h├áng phß║ºn tr─âm)
Theo d├Ái (0)Gß╗¡i c├óu trß║ú lß╗Øi Hß╗ºy -
Vß║¡n tß╗æc cß╗ºa mß╗Öt vß║¡t chuyß╗ân ─æß╗Öng l├á \(v\left( t \right) = {1 \over {2\pi }} + {{\sin \left( {\pi t} \right)} \over \pi }\left( {m/s} \right)\) T├¡nh qu├úng ─æã░ß╗Øng di chuyß╗ân cß╗ºa vß║¡t ─æ├│ trong khoß║úng thß╗Øi gian 1,5 gi├óy (l├ám tr├▓n kß║┐t quß║ú ─æß║┐n h├áng phß║ºn tr─âm).
25/05/2021 | 1 Trß║ú lß╗Øi
Vß║¡n tß╗æc cß╗ºa mß╗Öt vß║¡t chuyß╗ân ─æß╗Öng l├á \(v\left( t \right) = {1 \over {2\pi }} + {{\sin \left( {\pi t} \right)} \over \pi }\left( {m/s} \right)\) T├¡nh qu├úng ─æã░ß╗Øng di chuyß╗ân cß╗ºa vß║¡t ─æ├│ trong khoß║úng thß╗Øi gian 1,5 gi├óy (l├ám tr├▓n kß║┐t quß║ú ─æß║┐n h├áng phß║ºn tr─âm).
Theo d├Ái (0)Gß╗¡i c├óu trß║ú lß╗Øi Hß╗ºy -
Tính \(\int\limits_{{1 \over e}}^e {\left| {\ln x} \right|dx} \)
Theo d├Ái (0)Gß╗¡i c├óu trß║ú lß╗Øi Hß╗ºy -
Giß║ú sß╗¡ M v├á m theo thß╗® tß╗▒ l├á g├íi trß╗ï lß╗øn nhß║Ñ v├á nhß╗Å nhß║Ñt cß╗ºa h├ám sß╗æ f tr├¬n ─æoß║ín [a;b]. Chß╗®ng minh rß║▒ng: \(m\left( {b - a} \right) \le \int\limits_a^b {f\left( x \right)dx \ge M\left( {b - a} \right)} \)
24/05/2021 | 1 Trß║ú lß╗Øi
Giß║ú sß╗¡ M v├á m theo thß╗® tß╗▒ l├á g├íi trß╗ï lß╗øn nhß║Ñ v├á nhß╗Å nhß║Ñt cß╗ºa h├ám sß╗æ f tr├¬n ─æoß║ín [a;b]. Chß╗®ng minh rß║▒ng: \(m\left( {b - a} \right) \le \int\limits_a^b {f\left( x \right)dx \ge M\left( {b - a} \right)} \).
Theo d├Ái (0)Gß╗¡i c├óu trß║ú lß╗Øi Hß╗ºy -
Tính tích phân sau: \(\int\limits_{ - 2}^0 {\left( {x - {e^{ - x}}} \right)dx} \)
25/05/2021 | 1 Trß║ú lß╗Øi
Tính tích phân sau: \(\int\limits_{ - 2}^0 {\left( {x - {e^{ - x}}} \right)dx} \)
Theo d├Ái (0)Gß╗¡i c├óu trß║ú lß╗Øi Hß╗ºy -
Tính tích phân sau: \(\int\limits_2^5 {{{\left( {3x - 4} \right)}^4}dx} \).
25/05/2021 | 1 Trß║ú lß╗Øi
Tính tích phân sau: \(\int\limits_2^5 {{{\left( {3x - 4} \right)}^4}dx} \).
Theo d├Ái (0)Gß╗¡i c├óu trß║ú lß╗Øi Hß╗ºy -
Tính tích phân sau: \(\int\limits_0^1 {\left( {{e^{2x}} + {3 \over {x + 1}}} \right)dx} \).
25/05/2021 | 1 Trß║ú lß╗Øi
Tính tích phân sau: \(\int\limits_0^1 {\left( {{e^{2x}} + {3 \over {x + 1}}} \right)dx} \).
Theo d├Ái (0)Gß╗¡i c├óu trß║ú lß╗Øi Hß╗ºy -
Tính tích phân sau: \(\int\limits_2^4 {{{\left( {x + {1 \over x}} \right)}^2}dx} \).
24/05/2021 | 1 Trß║ú lß╗Øi
Tính tích phân sau: \(\int\limits_2^4 {{{\left( {x + {1 \over x}} \right)}^2}dx} \).
Theo d├Ái (0)Gß╗¡i c├óu trß║ú lß╗Øi Hß╗ºy -
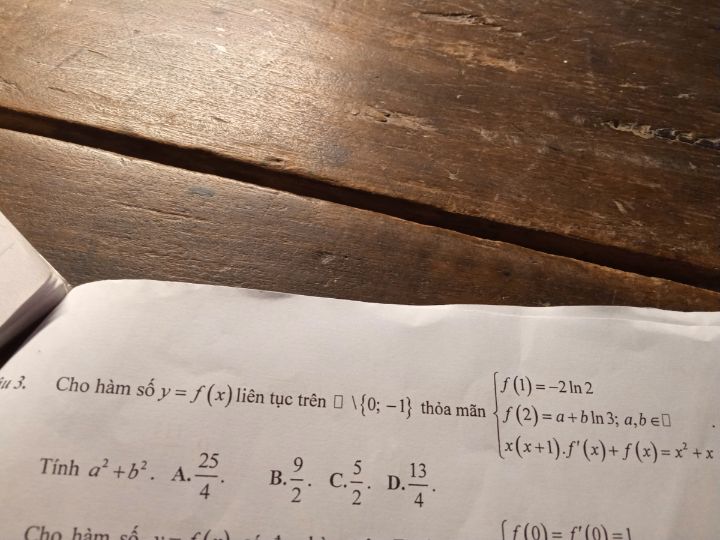 Theo d├Ái (0)Gß╗¡i c├óu trß║ú lß╗Øi Hß╗ºy
Theo d├Ái (0)Gß╗¡i c├óu trß║ú lß╗Øi Hß╗ºy -
\(\int\limits_0^1 {\sin \sqrt x dx} \) bß║▒ng ─æ├íp ├ín n├áo dã░ß╗øi ─æ├óy?
10/05/2021 | 1 Trß║ú lß╗Øi
A. \(2\left( {\sin 1 - \cos 1} \right)\)
B. \(\sin 1 - \cos 1\)
C. \(2\left( {\cos 1 - \sin 1} \right)\)
D. \(2\left( {\sin 1 + \cos 1} \right)\)
Theo d├Ái (0)Gß╗¡i c├óu trß║ú lß╗Øi Hß╗ºy -
─Éß╗æi vß╗øi t├¡ch ph├ón \(\int\limits_0^{\dfrac{\pi }{4}} {\dfrac{{\tan x}}{{{{\cos }^2}x}}dx} \), thß╗▒c hiß╗çn ─æß╗òi biß║┐n sß╗æ \(t = \tan x\) ta ─æã░ß╗úc:
09/05/2021 | 1 Trß║ú lß╗Øi
A. \(\int\limits_0^{\dfrac{\pi }{4}} {tdt} \)
B. \(\int\limits_{ - 1}^0 {tdt} \)
C. \(\int\limits_0^1 {tdt} \)
D. \( - \int\limits_0^1 {tdt} \)
Theo d├Ái (0)Gß╗¡i c├óu trß║ú lß╗Øi Hß╗ºy




