Hướng dẫn Giải bài tập Toán 11 Kết nối tri thức Chương 7 Bài 23 Đường thẳng vuông góc với mặt phẳng môn Toán học lớp 11 giúp các em học sinh nắm vững phương pháp giải bài tập và ôn luyện tốt kiến thức.
-
Hoạt động 1 trang 31 SGK Toán 11 Kết nối tri thức tập 2 - KNTT
Đối với cánh cửa như trong Hình 7.10, khi đóng – mở cánh cửa, ta coi mép dưới BC của cánh cửa luôn sát sàn nhà (khe hở không đáng kể).
a) Từ quan sát trên, hãy giải thích vì sao đường thẳng AB vuông góc với mọi đường thẳng đi qua B trên sàn nhà.
b) Giải thích vì sao đường thẳng AB vuông góc với mọi đường thẳng trên sàn nhà.

-
Hoạt động 2 trang 32 SGK Toán 11 Kết nối tri thức tập 2 - KNTT
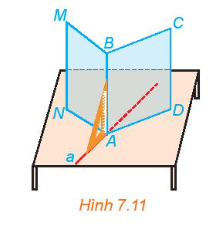
Gấp tấm bìa cứng hình chữ nhật sao cho nếp gấp chia tấm bia thành hai hình chữ nhật, sau đó đặt nó lên mặt bàn như Hình 7.11.
a) Bằng cách trên, ta tạo được đường thẳng AB vuông góc với hai đường thẳng nào thuộc mặt bàn?
b) Trên mặt bàn, qua điểm A kẻ một đường thẳng a tuỳ ý. Dùng ê ke, hãy kiểm tra trên mô hình xem AB có vuông góc với a hay không.
-
Luyện tập 1 trang 32 SGK Toán 11 Kết nối tri thức tập 2 - KNTT
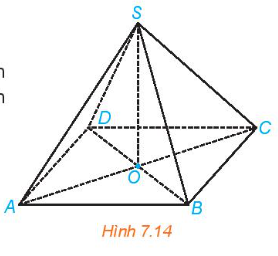
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành tâm O, SA = SC và SB = SD (H.7.14). Chứng minh rằng \(SO\perp (ABCD)\).
-
Vận dụng trang 33 SGK Toán 11 Kết nối tri thức tập 2 - KNTT
Khi làm cột treo quần áo, ta có thể tạo hai thanh đế thẳng đặt dưới sàn nhà và dựng cột treo vuông góc với hai thanh đế đó (H.7.15). Hãy giải thích vì sao bằng cách đó ta có được cột treo vuông góc với sàn nhà.

- VIDEOYOMEDIA
-
Hoạt động 3 trang 33 SGK Toán 11 Kết nối tri thức tập 2 - KNTT
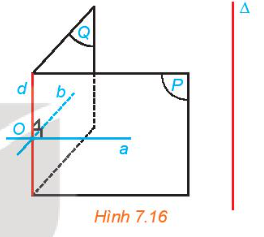
Cho điểm O và đường thẳng \(\Delta \) không đi qua O. Gọi d là đường thẳng đi qua O và song song với \(\Delta \). Xét hai mặt phẳng phân biệt tuỳ ý (P) và (Q) cùng chứa d. Trong các mặt phẳng (P), (Q) tương ứng kẻ các đường thẳng a, b cùng đi qua O và vuông góc với d (H.7.16). Giải thích vì sao mp(a, b) đi qua O và vuông góc với \(\Delta \).
-
Hoạt động 4 trang 34 SGK Toán 11 Kết nối tri thức tập 2 - KNTT
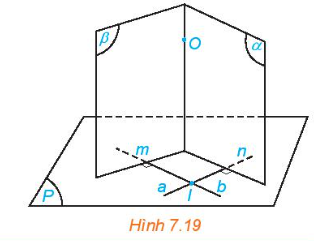
Cho mặt phẳng (P) và điểm O. Trong mặt phẳng (P), lấy hai đường thẳng cắt nhau a, b tuỳ ý. Gọi (\(\alpha \)),(\(\beta\)) là các mặt phẳng qua O và tương ứng vuông góc với a, b (H.7.19).
a) Giải thích vì sao hai mặt phẳng (\(\alpha \)),(\(\beta\)) cắt nhau theo một đường thẳng đi qua O.
b) Nêu nhận xét về mối quan hệ giữa \(\Delta \) và (P).
-
Luyện tập 2 trang 34 SGK Toán 11 Kết nối tri thức tập 2 - KNTT
Cho ba điểm phân biệt A, B, C sao cho các đường thẳng AB và AC cùng vuông góc với một mặt phẳng (P). Chứng minh rằng ba điểm A, B, C thẳng hàng.
-
Hoạt động 5 trang 34 SGK Toán 11 Kết nối tri thức tập 2 - KNTT
Cho đường thẳng a vuông góc với mặt phẳng (P) và song song với đường thẳng b. Lấy một đường thẳng m bất kì thuộc mặt phẳng (P). Tính (b, m) và từ đó rút ra mối quan hệ giữa b và (P).
-
Hoạt động 6 trang 34 SGK Toán 11 Kết nối tri thức tập 2 - KNTT
Cho hai đường thẳng phân biệt a và b cùng vuông góc với mặt phẳng (P). Xét O là một điểm thuộc a nhưng không thuộc b. Gọi c là đường thẳng qua O và song song với b.
a) Hỏi c có vuông góc với (P) hay không? Nêu nhận xét về vị trí tương đối giữa a và c.
b) Nêu nhận xét về vị trí tương đối giữa hai đường thẳng a và b.
-
Hoạt động 7 trang 35 SGK Toán 11 Kết nối tri thức tập 2 - KNTT
Cho hai mặt phẳng (P) và (Q) song song với nhau và đường thẳng \(\Delta \) vuông góc với (P). Gọi b là một đường thẳng bất kì thuộc (Q). Lấy một đường thẳng a thuộc (P) sao cho a song song với b (H.7.23). So sánh (\(Delta \), b) và (\(Delta \), a). Từ đó rút ra mối quan hệ giữa \(\Delta \) và (Q).
-
Hoạt động 8 trang 35 SGK Toán 11 Kết nối tri thức tập 2 - KNTT
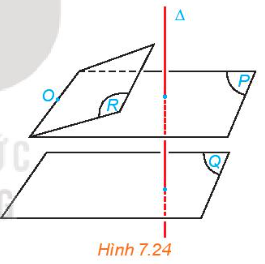
Cho hai mặt phẳng phân biệt (P) và (Q) cùng vuông góc với đường thẳng \(\Delta\) . Xét O là một điểm thuộc mặt phẳng (P) nhưng không thuộc mặt phẳng (Q). Gọi (R) là mặt phẳng đi qua O và song song với (Q) (H.7.24).
a) Hỏi (R) có vuông góc với \(\Delta\) hay không? Nêu nhận xét về vị trí tương đối giữa (P) và (R).
b) Nêu vị trí tương đối giữa (P) và (Q).
-
Luyện tập 3 trang 35 SGK Toán 11 Kết nối tri thức tập 2 - KNTT
Một chiếc bàn có các chân cùng vuông góc với mặt phẳng chứa mặt bàn và mặt phẳng chứa mặt sàn. Hỏi hai mặt phẳng đó có song song với nhau hay không? Vì sao?
-
Hoạt động 9 trang 35 SGK Toán 11 Kết nối tri thức tập 2 - KNTT
Cho đường thẳng a song song với mặt phẳng (P) và đường thẳng \(\Delta\) vuông góc với mặt phẳng (P). Tính (\(\Delta\), a).
-
Hoạt động 10 trang 36 SGK Toán 11 Kết nối tri thức tập 2 - KNTT
Cho đường thẳng a và mặt phẳng (P) cùng vuông góc với một đường thẳng Δ.
a) Qua một điểm O thuộc (P), kẻ đường thẳng a song song với a. Nêu vị trí tương đối giữa a' và (P).
b) Nêu vị trí tương đối giữa a và (P).
-
Luyện tập 4 trang 36 SGK Toán 11 Kết nối tri thức tập 2 - KNTT
Cho hình chóp S.ABCD có đáy ABCD là một hình vuông, SA⊥(ABCD). Kẻ AH vuông góc với SC (H thuộc SC), BM vuông góc với SC (M thuộc SC). Chứng minh rằng SC⊥(MBD) và AH // (MBD).
-
Giải Bài 7.5 trang 36 SGK Toán 11 Kết nối tri thức tập 2 - KNTT
Cho hình chóp S.ABC có đáy là tam giác cân tại A và \(SA\perp (ABC)\). Gọi M là trung điểm của BC. Chứng minh rằng:
a) \(BC\perp (SAM)\);
b) Tam giác SBC cân tại S.
-
Giải Bài 7.6 trang 36 SGK Toán 11 Kết nối tri thức tập 2 - KNTT
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật và SA⊥(ABCD). Chứng minh rằng các mặt bên của hình chóp S.ABCD là các tam giác vuông.
-
Giải Bài 7.7 trang 36 SGK Toán 11 Kết nối tri thức tập 2 - KNTT
Cho hình chóp S.ABCD có đáy là hình chữ nhật và \(SA \perp (ABCD)\). Gọi M, N tương ứng là hình chiếu của A trên SB, SD. Chứng minh rằng:
\(AM \perp (SBC)\), \(AN \perp (SCD)\), \(SC\perp (AMN)\).
-
Giải Bài 7.8 trang 36 SGK Toán 11 Kết nối tri thức tập 2 - KNTT
Bạn Vinh thả quả dọi chìm vào thùng nước. Hỏi khi dây dọi căng và mặt nước yên lặng thì đường thẳng chứa dây dọi có vuông góc với mặt phẳng chứa mặt nước trong thùng hay không?
-
Giải Bài 7.9 trang 36 SGK Toán 11 Kết nối tri thức tập 2 - KNTT
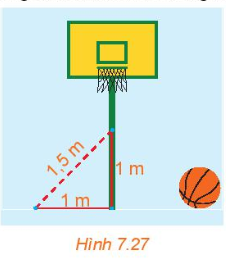
Một cột bóng rổ được dựng trên một sân phẳng. Bạn Hùng đo khoảng cách từ một điểm trên sân, cách chân cột 1 m đến một điểm trên cột, cách chân cột 1 m được kết quả là 1,5 m (H.7.27). Nếu phép đo của Hùng là chính xác thì cột có vuông góc với sân hay không? Có thể kết luận rằng cột không có phương thẳng đứng hay không?
-
Bài tập 7.6 trang 28 SBT Toán 11 Tập 2 Kết nối tri thức - KNTT
Cho hình chóp \(S.ABC\) có \(SA\) vuông góc với mặt phẳng \(\left( {ABC} \right)\) và đáy là tam giác \(ABC\) vuông tại\(B\). Kẻ \(AM\) vuông góc với \(SB\) tại \(M\) và \(AN\) vuông góc với \(SC\) tại\(N\). Chứng minh rằng:
a) \(BC \bot \left( {SAB} \right)\);
b) \(AM \bot \left( {SBC} \right)\);
c) \(SC \bot \left( {AMN} \right)\).
-
Bài tập 7.7 trang 28 SBT Toán 11 Tập 2 Kết nối tri thức - KNTT
Cho tứ diện \(OABC\) có ba cạnh \(OA,OB,OC\) đôi một vuông góc với nhau. Gọi \(H\) là chân đường vuông góc hạ từ \(O\) đến mặt phẳng\(\left( {ABC} \right)\). Chứng minh rằng:
a) \(BC \bot \left( {OAH} \right)\);
b) \(H\) là trực tâm của tam giác \(ABC\);
c) \(\frac{1}{{O{H^2}}} = \frac{1}{{O{A^2}}} + \frac{1}{{O{B^2}}} + \frac{1}{{O{C^2}}}\).
-
Bài tập 7.8 trang 28 SBT Toán 11 Tập 2 Kết nối tri thức - KNTT
Cho tứ diện \(ABCD\) có \(AB = AC\) và \(DB = DC\). Chứng minh rằng \(AD \bot BC\)?
-
Bài tập 7.9 trang 28 SBT Toán 11 Tập 2 Kết nối tri thức - KNTT
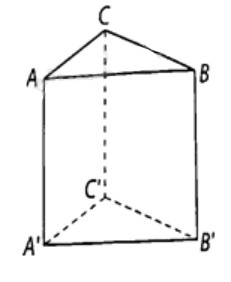
Cho hình lăng trụ tam giác \(ABC \cdot A'B'C'\) có \(AA'\) vuông góc với mặt phẳng \(\left( {ABC} \right)\) và đáy là tam giác \(ABC\) vuông tại \(B\). Chứng minh rằng:
a) \(B'B \bot \left( {A'B'C'} \right)\);
b) \(B'C \bot \left( {ABB'A'} \right)\).
-
Bài tập 7.10 trang 28 SBT Toán 11 Tập 2 Kết nối tri thức - KNTT
Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình thoi tâm \(O\) và \(SA = SC\), \(SB = SD\). Chứng minh rằng:
a) \(SO \bot \left( {ABCD} \right)\);
b) \(AC \bot \left( {SBD} \right)\) và \(BD \bot \left( {SAC} \right)\).
-
Bài tập 7.11 trang 28 SBT Toán 11 Tập 2 Kết nối tri thức - KNTT
Cho hình chóp \(S.ABC\) có \(SA \bot \left( {ABC} \right)\), tam giác \(ABC\) nhọn. Gọi \(H,K\) lần lượt là trực tâm của tam giác \(ABC\) và \(SBC\). Chứng minh rằng:
a) \(BC \bot \left( {SAH} \right)\) và các đường thẳng \(AH,BC,SK\) đồng quy;
b) \(SB \bot \left( {CHK} \right)\) và \(HK \bot \left( {SBC} \right)\).
-
Bài tập 7.12 trang 28 SBT Toán 11 Tập 2 Kết nối tri thức - KNTT
Một cấy cột được dựng trên một sàn phẳng. Người ta thả dây dọi và ngắm thấy cột song song với dây dọi. Hỏi có thể khẳng định rằng cây cột vuông góc với sàn hay không? Vì sao?


