Bài tập 7.6 trang 28 SBT Toán 11 Tập 2 Kết nối tri thức - KNTT

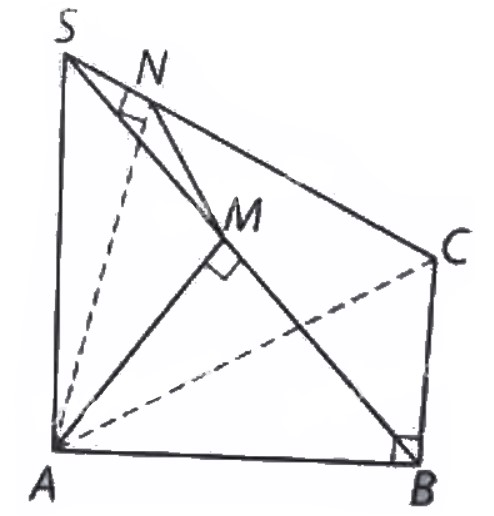
a) Ta có: \(BC \bot AB\)và \(SA \bot \left( {ABC} \right)\) nên\(SA \bot BC\), suy ra \(BC \bot \left( {SAB} \right).\)

b) Vì \(BC \bot \left( {SAB} \right).\) nên \(BC \bot AM.\), mà \(AM \bot SB.\), suy ra \(AM \bot \left( {SBC} \right).\)

c) Vì \(AM \bot \left( {SBC} \right).\) nên \(AM \bot SC.\), mà \(AN \bot SC.\), suy ra \(\left( {AMN} \right) \bot SC.\).

-- Mod Toán 11 HỌC247