Giải bài tập Toán 11 Chân trời sáng tạo Bài 1: Hai đường thẳng vuông góc

Ta đã biết cách xác định góc giữa hai đường thẳng cùng thuộc một mặt phẳng. Có góc giữa hai đường thẳng chéo nhau không? Nếu có, làm thế nào để xác định?

Cho hai đường thẳng chéo nhau \(a\) và \(b\) trong không gian. Qua một điểm \(M\) tuỳ ý vẽ \(a'\parallel a\) và vẽ \(b'\parallel b\). Khi thay đổi vị trí của điểm \(M\), có nhận xét gì về góc giữa \(a'\) và \(b'\)?

Cho hình hộp \(ABCD.A'B'C'D'\) có 6 mặt đều là hình vuông \(M,N,E,F\) lần lượt là trung điểm các cạnh \(BC,BA,AA',A'D'\). Tính góc giữa các cặp đường thẳng:

a) \(MN\) và \(DD'\);

b) \(MN\) và \(CD'\);

c) \(EF\) và \(CC'\).

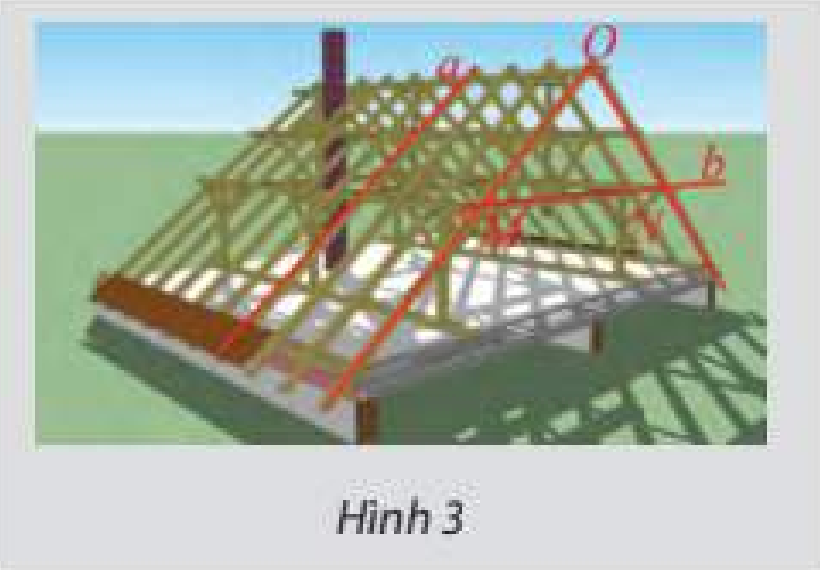
Khung của một mái nhà được ghép bởi các thanh gỗ như Hình 3. Cho biết tam giác \(OMN\) vuông cân tại \(O\). Tính góc giữa hai thanh gỗ \(a\) và \(b\).

Cho hình hộp \(ABCD.A'B'C'D'\) có 6 mặt đều là hình vuông. Nêu nhận xét về góc giữa các cặp đường thẳng:

Cho hình hộp \(ABCD.A'B'C'D'\) có 6 mặt đều là hình vuông. Nêu nhận xét về góc giữa các cặp đường thẳng:

a) \(AB\) và \(BB'\);

b) \(AB\) và \(DD'\).

Cho hình hộp \(ABCD.A'B'C'D'\) có 6 mặt đều là hình vuông.

a) Tìm các đường thẳng đi qua hai đỉnh của hình lập phương và vuông góc với \(AC\).

b) Trong các đường thẳng tìm được ở câu a, tìm đường thẳng chéo với \(AC\).

Hình bên mô tả một người thợ đang ốp gạch vào tưởng có sử dụng thước laser để kẻ vạch. Tìm các đường thẳng vuông góc với đường thẳng \(a\) trong Hình 4.

Cho hình chóp \(S.ABCD\) có đáy là hình thoi \(ABCD\) cạnh \(a\). Cho biết \(SA = a\sqrt 3 ,SA \bot AB\) và \(SA \bot A{\rm{D}}\). Tính góc giữa \(SB\) và \(C{\rm{D}}\), \(S{\rm{D}}\) và \(C{\rm{B}}\).

Cho tứ diện đều \(ABCD\). Chứng minh rằng \(AB \bot CD\).

Cho hình chóp \(S.ABC\) có \(SA = SB = SC = a,\widehat {BSA} = \widehat {CSA} = {60^ \circ },\) \(\widehat {BSC} = {90^ \circ }\). Cho \(I\) và \(J\) lần lượt là trung điểm của \(SA\) và \(BC\). Chứng minh rằng \(IJ \bot SA\) và \(IJ \bot BC\).

Cho tứ diện đều \(ABCD\) cạnh \(a\). Gọi \(K\) là trung điểm của \(CD\). Tính góc giữa hai đường thẳng \(AK\) và \(BC\).

Cho tứ diện \(ABCD\). Gọi \(M,N\) lần lượt là trung điểm của \(BC\) và \(A{\rm{D}}\). Biết \(AB = CD = 2a\) và \(MN = a\sqrt 3 \). Tính góc giữa \(AB\) và \(C{\rm{D}}\).

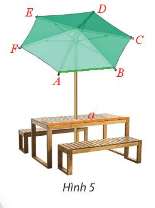
Một ô che nắng có viền khung hình lục giác đều \(ABCDEF\) song song với mặt bàn và có cạnh \(AB\) song song với cạnh bàn \(a\) (Hình 5). Tinh số đo góc hợp bởi đường thẳng \(a\) lần lượt với các đường thẳng \(AF,AE\) và \(A{\rm{D}}\).

Cho tứ diện đều ABCD, M là trung điểm của cạnh BC. Tính góc giữa AB và DM?

Cho hình chóp S.ABCD. có đáy là hình thoi cạnh a, SA = $a\sqrt{3}$, SA $\perp$ AC, SA $\perp$ BC, $\widehat{BAD}$= 120°. Gọi M, N lần lượt là trung điểm của AD, BC. Tính góc giữa các cặp đường thẳng:

a) SD và BC.

b) MN và SC.

Cho tứ diện ABCD có AB = CD, AC = BD, AD = BC.

a) Chứng minh đoạn nối các trung điểm của các cặp cạnh đối thì vuông góc với hai cạnh đó.

b) Chứng minh hai đoạn nối các trung điểm của các cặp cạnh đối thì vuông góc với nhau.

Cho hình chóp tứ giác S.ABCD có tất cả các cạnh đều bằng a. Gọi M, N, I, J lần lượt là trung điểm của SA, SD, SC và BC. Tính góc giữa các cặp đường thẳng sau:

a) IJ và DC;

b) MN và IJ.

Cho tứ diện đều ABCD cạnh a. Gọi O là tâm đường tròn ngoại tiếp tam giác BCD. Chứng minh hai đường thẳng OA và CD vuông góc với nhau?