Bài tập 1 trang 50 SBT Toán 11 Tập 2 Chân trời sáng tạo - CTST

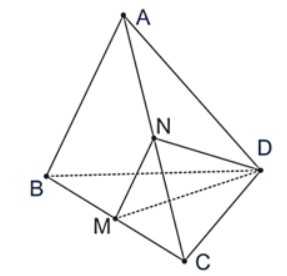
Cho N là trung điểm của cạnh AC.

$\Rightarrow$ MN là đường trung trực của ∆ABC.

$\Rightarrow$ MN // AB $\iff$ (AB, DM) = (MN, DM) = $\widehat{DMN}$ .

Lại có: ∆BCD và ∆ACD là các tam giác đều (theo giả thiết).

Giả sử ABCD là tứ diện đều cạnh a.

$\Rightarrow$ DM = DN = $\frac{a\sqrt{3}}{2}$ ; MN = $\frac{AB}{2}$ = $\frac{a}{2}$.

Áp dụng định lý hàm cos trong ∆DMN, ta có:

$\cos \widehat{DMN}=\frac{D{M}^2+M{N}^2-D{N}^2}{2.DM.MN}=\frac{\sqrt{3}}{6}$.

Do đó (AB, DM) = $\widehat{DMN}$ ≈ 73,22°.

-- Mod Toán 11 HỌC247