Bài tập 2 trang 51 SBT Toán 11 Tập 2 Chân trời sáng tạo
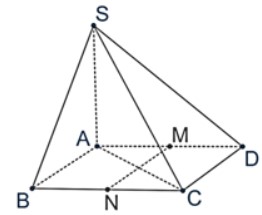
Cho hình chóp S.ABCD. có đáy là hình thoi cạnh a, SA = , SA AC, SA BC, = 120°. Gọi M, N lần lượt là trung điểm của AD, BC. Tính góc giữa các cặp đường thẳng:
a) SD và BC.
b) MN và SC.
Hướng dẫn giải chi tiết Bài tập 2
a) Ta có: \(\left\{ \begin{matrix} SA\bot AC \\ SA\bot BC \\ \end{matrix} \right.\)
SA ⊥ (ABCD) SA ⊥ AD.
Do BC // AD nên (BC, SD) = (AD, SD).
Do đó = 60°.
b) Do MN // CD nên (SD, MN) = (SD, CD) = .
Áp dụng định lí Pythagore, ta có:
\(\left\{ \begin{matrix} SD=\sqrt{S{{A}^{2}}+A{{D}^{2}}}=\sqrt{{{\left( a\sqrt{3} \right)}^{2}}+{{a}^{2}}}=2a \\ SC=\sqrt{S{{A}^{2}}+A{{C}^{2}}}=\sqrt{{{\left( a\sqrt{3} \right)}^{2}}+{{a}^{2}}}=2a \\ \end{matrix} \right.\)
Áp dụng định lí hàm cos trong ∆SCD, ta có:
.
Do đó (SD, MN) = ≈ 75,52°.
-- Mod Toán 11 HỌC247
Bài tập SGK khác
Giải Bài 6 trang 56 SGK Toán 11 Chân trời sáng tạo tập 2 - CTST
Bài tập 1 trang 50 SBT Toán 11 Tập 2 Chân trời sáng tạo - CTST
Bài tập 3 trang 51 SBT Toán 11 Tập 2 Chân trời sáng tạo - CTST
Bài tập 4 trang 51 SBT Toán 11 Tập 2 Chân trời sáng tạo - CTST
Bài tập 5 trang 44 SBT Toán 11 Tập 2 Chân trời sáng tạo - CTST
Chưa có câu hỏi nào. Em hãy trở thành người đầu tiên đặt câu hỏi.


