Bài tập 5 trang 44 SBT Toán 11 Tập 2 Chân trời sáng tạo - CTST

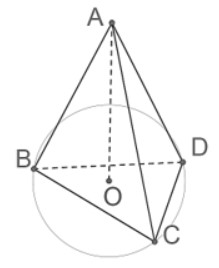
Giả sử điểm H là chân đường vuông góc hạ từ đỉnh A xuống mặt phẳng đáy.

Xét ∆AHB, ∆AHC và ∆AHD:

\(\left\{ \begin{matrix} AB=AC=AD=a \\ \begin{align} & AH~~chung \\ & \widehat{AHB}=\widehat{AHC}=\widehat{AHD}={{90}^{o}} \\ \end{align} \\ \end{matrix} \right.\)

$\Rightarrow$ ∆AHB, ∆AHC và ∆AHD là các tam giác bằng nhau (cạnh huyền – cạnh góc vuông).

$\Rightarrow$ BH = CH = DH $\Rightarrow$ H là tâm đường tròn ngoại tiếp tam giác BCD.

$\Rightarrow$ H $\equiv$ O$\iff$ AO là đường cao của tứ diện ABCD.

$\Rightarrow$ OA ⊥ CD.

Vậy hai đường thẳng OA và CD vuông góc với nhau.

-- Mod Toán 11 HỌC247