Giải Bài 1 trang 56 SGK Toán 11 Chân trời sáng tạo tập 2 - CTST

Lời giải chi tiết

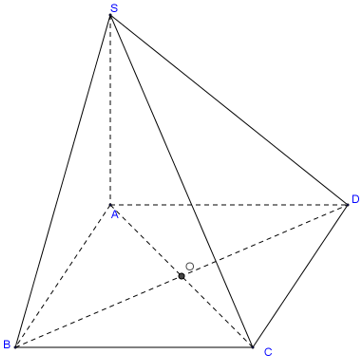
a) Ta có: \(C{\rm{D}}\parallel AB \Rightarrow \left( {SB,C{\rm{D}}} \right) = \left( {SB,AB} \right) = \widehat {SBA}\).

\(\tan \widehat {SBA} = \frac{{SA}}{{AB}} = \frac{{a\sqrt 3 }}{a} = \sqrt 3 \Rightarrow \widehat {SBA} = {60^ \circ }\)

Vậy \(\left( {SB,C{\rm{D}}} \right) = {60^ \circ }\).

b) Ta có: \(C{\rm{B}}\parallel AD \Rightarrow \left( {SD,C{\rm{B}}} \right) = \left( {SD,AD} \right) = \widehat {S{\rm{D}}A}\).

\(\tan \widehat {SDA} = \frac{{SA}}{{AD}} = \frac{{a\sqrt 3 }}{a} = \sqrt 3 \Rightarrow \widehat {SDA} = {60^ \circ }\)

Vậy \(\left( {SD,C{\rm{B}}} \right) = {60^ \circ }\).

-- Mod Toán 11 HỌC247