Hướng dẫn Giải bài tập Toán 11 Cánh Diều Chương 6 Bài 1 Phép tính luỹ thừa với số mũ thực môn Toán học lớp 11 thực giúp các em học sinh nắm vững phương pháp giải bài tập và ôn luyện tốt kiến thức.
-
Khởi động trang 27 SGK Toán 11 Tập 2 Cánh diều - CD
Ở các lớp dưới, ta đã làm quen với phép tính lũy thừa với số mũ tự nhiên của một số thực và các tính chất của phép tính lũy thừa đó. Những khái niệm lũy thừa với số mũ nguyên, số mũ hữu tỉ và số mũ thực của một số thực được xây dựng như thế nào? Những phép lũy thừa đó có tính chất gì?
-
Hoạt động 1 trang 27 SGK Toán 11 Tập 2 Cánh diều - CD
a) Cho n là một số nguyên dương. Với a là số thực tùy ý, nêu định nghĩa lũy thừa bậc n của a.
b) Với a là số thực tùy ý khác 0, nêu quy ước xác định lũy thừa bậc 0 của a.
-
Luyện tập 1 trang 28 SGK Toán 11 Tập 2 Cánh diều - CD
Tính giá trị của biểu thức:
-
Hoạt động 2 trang 28 SGK Toán 11 Tập 2 Cánh diều - CD
a) Với a là số thực không ân, nêu định nghĩa căn bậc hai của a.
b) Với a là số thực tùy ý, nêu định nghĩa căn bậc ba của a.
- VIDEOYOMEDIA
-
Luyện tập 2 trang 28 SGK Toán 11 Tập 2 Cánh diều - CD
Các số 2 và –2 có phải là căn bậc 6 của 64 hay không?
-
Hoạt động 3 trang 29 SGK Toán 11 Tập 2 Cánh diều - CD
a) Với mỗi số thực a, so sánh: và |a|; và a.
b) Cho a, b là hai số thực dương. So sánh và
-
Luyện tập 3 trang 29 SGK Toán 11 Tập 2 Cánh diều - CD
Rút gọn mỗi biểu thức sau:
a)
b)
-
Hoạt động 4 trang 29 SGK Toán 11 Tập 2 Cánh diều - CD
Thực hiện các hoạt động sau:
a) So sánh \(2^{\frac{6}{3}}\) và 22;
b) So sánh \(2^{\frac{6}{3}}\) và
-
Luyện tập 4 trang 30 SGK Toán 11 Tập 2 Cánh diều - CD
Rút gọn mỗi biểu thức:
-
Hoạt động 5 trang 30 SGK Toán 11 Tập 2 Cánh diều - CD
Xét số vô tỉ
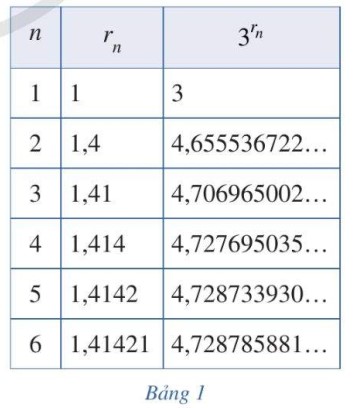
Xét dãy số hữu tỉ r1 = 1; r2 = 1,4; r3 = 1,41; r4 = 1,414; r5 = 1,4142; r6 = 1,41421; ...và Bằng cách tính tương ứng, ta nhận được Bảng 1 ghi các dãy số (rn) và với n = 1, 2, ..., 6. Người ta chứng minh được rằng khi n → +∞ thì dãy số dần đến một giới hạn mà ta gọi là
Nêu dự đoán về giá trị của số (đến hàng phần trăm).
-
Luyện tập 5 trang 31 SGK Toán 11 Tập 2 Cánh diều - CD
So sánh và 10?
-
Hoạt động 6 trang 31 SGK Toán 11 Tập 2 Cánh diều - CD
Nêu những tính chất của phép tính lũy thừa với số mũ nguyên của một số thực dương?
-
Luyện tập 6 trang 32 SGK Toán 11 Tập 2 Cánh diều - CD
Không sử dụng máy tính cầm tay, hãy so sánh các số và
-
Luyện tập 7 trang 32 SGK Toán 11 Tập 2 Cánh diều - CD
Dùng máy tính cầm tay để tính (làm tròn kết quả đến hàng phần trăm):
a)
b)
-
Bài 1 trang 33 SGK Toán 11 Tập 2 Cánh diều - CD
Tính:
a)
b)
c)
-
Bài 2 trang 33 SGK Toán 11 Tập 2 Cánh diều - CD
Cho a, b là những số thực dương. Viết các biểu thức sau dưới dạng lũy thừa với số mũ hữu tỉ:
a)
b)
c)
d)
-
Bài 3 trang 33 SGK Toán 11 Tập 2 Cánh diều - CD
Rút gọn mỗi biểu thức sau:
a)
b)
-
Bài 4 trang 33 SGK Toán 11 Tập 2 Cánh diều - CD
Viết các số sau theo thứ tự tăng dần:
a)
b)
-
Bài 5 trang 33 SGK Toán 11 Tập 2 Cánh diều - CD
Không sử dụng máy tính cầm tay, hãy so sánh các số sau:
a) \(6^{\sqrt{3}}\) và 36;
b) \(0,2^{\sqrt{3}}\) và \(0,2^{\sqrt{5}}\).
-
Bài 6 trang 33 SGK Toán 11 Tập 2 Cánh diều - CD
Định luật thứ ba của Kepler về quỹ đạo chuyển động cho biết cách ước tính khoảng thời gian P (tính theo năm Trái Đất) mà một hành tinh cần để hoàn thành một quỹ đạo quay quanh Mặt Trời. Khoảng thời gian đó được xác định bởi hàm số trong đó d là khoảng cách từ hành tinh đó đến Mặt Trời tính theo đơn vị thiên văn AU (1 AU là khoảng cách từ Trái Đất đến Mặt Trời, tức là 1 AU khoảng 93 000 000 dặm) (Nguồn: R.I. Charles et al., Algebra 2, Pearson). Hỏi Sao Hỏa quay quanh Mặt Trời thì mất bao nhiêu năm Trái Đất (làm tròn kết quả đến hàng phần trăm)? Biết khoảng cách từ Sao Hỏa đến Mặt Trời là 1,52 AU.
-
Bài tập 1 trang 33 SBT Toán 11 Tập 2 Cánh diều - CD
Điều kiện xác định của \({x^{ - 7}}\) là:
A. \(x \in \mathbb{R}\)
B. \(x \ne 0\)
C. \(x \ge 0\)
D. \(x > 0\)
-
Bài tập 2 trang 34 SBT Toán 11 Tập 2 Cánh diều - CD
Điều kiện xác định của \(\sqrt[5]{{{x^3}}}\) là:
A. \(x \in \mathbb{R}\)
B. \(x \ne 0\)
C. \(x \ge 0\)
D. \(x > 0\)
-
Bài tập 3 trang 34 SBT Toán 11 Tập 2 Cánh diều - CD
Điều kiện xác định của \(\sqrt[8]{{{x^3}}}\) là:
A. \(x \in \mathbb{R}\)
B. \(x \ne 0\)
C. \(x \ge 0\)
D. \(x > 0\)
-
Bài tập 4 trang 34 SBT Toán 11 Tập 2 Cánh diều - CD
Điều kiện xác định của \({x^{\sqrt 2 }}\) là:
A. \(x \in \mathbb{R}\)
B. \(x \ne 0\)
C. \(x \ge 0\)
D. \(x > 0\)
-
Bài tập 5 trang 34 SBT Toán 11 Tập 2 Cánh diều - CD
Giá trị của biểu thức \(P = {2^{1 - \sqrt 2 }}{.2^{3 + \sqrt 2 }}{.4^{\frac{1}{2}}}\) bằng:
A. \(128.\)
B. \(64.\)
C. \(16.\)
D. \(32.\)
-
Bài tập 6 trang 34 SBT Toán 11 Tập 2 Cánh diều - CD
Nếu a > 1 thì:
A. \({{a}^{-\sqrt{3}}}>\frac{1}{{{a}^{\sqrt{5}}}};\)
B. \({{a}^{-\sqrt{3}}}<\frac{1}{{{a}^{\sqrt{5}}}};\)
C. \({{a}^{-\sqrt{3}}}\le \frac{1}{{{a}^{\sqrt{5}}}};\)
D. \({{a}^{-\sqrt{3}}}=\frac{1}{{{a}^{\sqrt{5}}}}.\)
-
Bài tập 7 trang 34 SBT Toán 11 Tập 2 Cánh diều - CD
Nếu \({\left( {2 - \sqrt 3 } \right)^{a - 1}} < 2 + \sqrt 3 \) thì:
A. \(a > 0.\)
B. \(a > 1.\)
C. \(a < 1.\)
D. \(a < 0.\)
-
Bài tập 8 trang 34 SBT Toán 11 Tập 2 Cánh diều - CD
Nếu \({a^{\sqrt 3 }} < {a^{\sqrt 2 }}\) thì:
A. \(a > 1.\)
B. \(a < 1.\)
C. \(0 < a < 1.\)
D. \(a > 0.\)
-
Bài tập 9 trang 34 SBT Toán 11 Tập 2 Cánh diều - CD
Biểu thức \(P = \sqrt[3]{{{x^2}\sqrt {{x^3}} }}\) với \(x > 0\) được rút gọn bằng:
A. \(P = {x^{\frac{5}{3}}}\)
B. \(P = {x^{\frac{7}{6}}}\)
C. \(P = {x^{\frac{1}{3}}}\)
D. \(P = {x^{\frac{5}{6}}}\)
-
Bài tập 10 trang 34 SBT Toán 11 Tập 2 Cánh diều - CD
Biểu thức \(Q = {a^{\sqrt 3 }}.{\left( {\frac{1}{a}} \right)^{\sqrt 3 - 1}}\) với \(a > 0\) được rút gọn bằng:
A. \(\frac{1}{a}.\)
B. \({a^3}.\)
C. \(a.\)
D. \(1.\)
-
Bài tập 11 trang 34 SBT Toán 11 Tập 2 Cánh diều - CD
Viết các biểu thức sau về lũy thừa cơ số a, biết:
a) \(A = \sqrt[7]{{3.\sqrt[5]{{\frac{1}{3}}}}}\) với \(a = 3;\)
b) \(B = \frac{{25\sqrt[3]{5}}}{{\sqrt {125} }}\) với \(a = \sqrt 5 .\)
-
Bài tập 12 trang 34 SBT Toán 11 Tập 2 Cánh diều - CD
Không sử dụng máy tính cầm tay, so sánh hai số a và b, biết:
a) \(a = {\left( {\sqrt 3 - 1} \right)^{\sqrt 2 }}\) và \(b = {\left( {\sqrt 3 - 1} \right)^{\sqrt 3 }};\) b) \(a = {\left( {\sqrt 2 - 1} \right)^\pi }\) và \(b = {\left( {\sqrt 2 + 1} \right)^e};\)
c) \(a = \frac{1}{{{3^{400}}}}\) và \(b = \frac{1}{{{4^{300}}}};\)
d) \(a = \frac{8}{{\sqrt[4]{{27}}}}\) và \(b = {\left( {\frac{{\sqrt 3 }}{2}} \right)^{\frac{3}{4}}}.\)
-
Bài tập 13 trang 35 SBT Toán 11 Tập 2 Cánh diều - CD
Xác định các giá trị của số thực a thỏa mãn:
a) \({a^{\frac{1}{2}}} > {a^{\sqrt 3 }};\)
b) \({a^{ - \frac{3}{2}}} < {a^{\frac{2}{3}}};\)
c) \({\left( {\sqrt 2 } \right)^a} > {\left( {\sqrt 3 } \right)^a}.\)
-
Bài tập 14 trang 35 SBT Toán 11 Tập 2 Cánh diều - CD
Cho \(a > 0,{\rm{ }}b > 0\). Rút gọn mỗi biểu thức sau:
a) \(A = \frac{{{{\left( {\sqrt[4]{{{a^3}{b^2}}}} \right)}^4}}}{{\sqrt[3]{{\sqrt {{a^{12}}{b^6}} }}}};\)
b) \(B = \frac{{{a^{\frac{1}{3}}}\sqrt b + {b^{\frac{1}{3}}}\sqrt a }}{{\sqrt[6]{a} + \sqrt[6]{b}}}.\)
-
Bài tập 16 trang 35 SBT Toán 11 Tập 2 Cánh diều - CD
Một chất phóng xạ có chu kì bán rã là 25 năm, tức là cứ sau 25 năm, khối lượng của chất phóng xạ đó giảm đi một nửa. Giả sử lúc đầu có 10 g chất phóng xạ đó. Viết công thức tính khối lượng của chất đó còn lại sau t năm và tính khối lượng của chất đó còn lại sau 120 năm (làm tròn kết quả đến hàng phần nghìn theo đơn vi gam)?


