Giải bài 3 tr 91 sách GK Toán Hình lớp 11
Cho hình bình hành ABCD. Gọi S là một điểm nằm ngoài mặt phẳng chứa hình bình hành. Chứng minh rằng: \(\overrightarrow{SA}\) + \(\overrightarrow{SC}\) = \(\overrightarrow{SB}\) + \(\overrightarrow{SD}\).
Hướng dẫn giải chi tiết
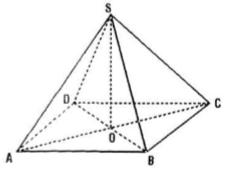
Gọi O là giao điểm của AC và BD ⇒ O là trung điểm của AC và BD.
Trong tam giác SAC, ta có O là trung điểm của AC.
-- Mod Toán 11 HỌC247
Video hướng dẫn giải SGK
Bài tập SGK khác
Bài tập 1 trang 91 SGK Hình học 11
Bài tập 2 trang 91 SGK Hình học 11
Bài tập 4 trang 91 SGK Hình học 11
Bài tập 5 trang 92 SGK Hình học 11
Bài tập 6 trang 92 SGK Hình học 11
Bài tập 7 trang 92 SGK Hình học 11
Bài tập 8 trang 92 SGK Hình học 11
Bài tập 9 trang 92 SGK Hình học 11
Bài tập 10 trang 92 SGK Hình học 11
Bài tập 3.1 trang 129 SBT Hình học 11
Bài tập 3.2 trang 129 SBT Hình học 11
Bài tập 3.3 trang 129 SBT Hình học 11
Bài tập 3.4 trang 130 SBT Hình học 11
Bài tập 3.5 trang 130 SBT Hình học 11
Bài tập 3.6 trang 130 SBT Hình học 11
Bài tập 3.7 trang 130 SBT Hình học 11
Bài tập 1 trang 91 SGK Hình học 11 NC
Bài tập 2 trang 91 SGK Toán 11 NC
Bài tập 3 trang 91 SGK Hình học 11 NC
Bài tập 4 trang 91 SGK Hình học 11 NC
-


Cho hình hộp \(ABCD.A'B'C'D'\). Chứng minh rằng: \(\overrightarrow{AB}\) + \(\overrightarrow{B'C'}\) + \(\overrightarrow{DD'}\) = \(\overrightarrow{AC'}\).
bởi Sasu ka
 25/02/2021
Theo dõi (0) 1 Trả lời
25/02/2021
Theo dõi (0) 1 Trả lời -


Cho hình hộp \(ABCD.EFGH\). Gọi \(I\) và \(K \) lần lượt là trung điểm của các cạnh \(AB\) và \(BC\). Chứng minh rằng các đường thẳng \(IK\) và \(ED\) song song với mặt phẳng \((AFC)\). Từ đó suy ra ba vecto \(\overrightarrow {{\rm{AF}}} ;\,\overrightarrow {IK} ;\,\overrightarrow {ED} \) đồng phẳng.
bởi Quế Anh
 25/02/2021
Theo dõi (0) 1 Trả lời
25/02/2021
Theo dõi (0) 1 Trả lời





