Giải bài 3.3 tr 129 SBT Hình học 11
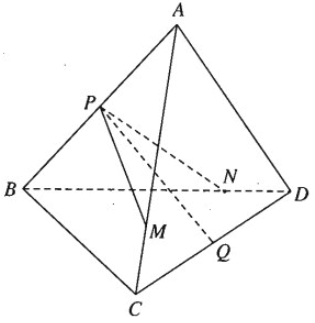
Cho tứ diện ABCD. Gọi P và Q lần lượt là trung điểm của các cạnh AB và CD. Trên các cạnh AC và BD lần lượt ta lấy các điểm M, N sao cho
\(\frac{{AM}}{{AC}} = \frac{{BN}}{{BD}} = k\left( {k > 0} \right)\)
Chứng minh rằng ba vectơ \(\overrightarrow {PQ} ,\overrightarrow {PM} ,\overrightarrow {PN} \) đồng phẳng.
Hướng dẫn giải chi tiết
Ta có:
\(\begin{array}{l}
\overrightarrow {PQ} = \frac{1}{2}\left( {\overrightarrow {PC} + \overrightarrow {PD} } \right) = \frac{1}{2}\left[ {\left( {\overrightarrow {AC} - \overrightarrow {AP} } \right) + \left( {\overrightarrow {BD} - \overrightarrow {BP} } \right)} \right]\\
= \frac{1}{2}\left[ {\left( {\overrightarrow {AC} + \overrightarrow {BD} } \right) - \underbrace {\left( {\overrightarrow {AP} + \overrightarrow {BP} } \right)}_{\overrightarrow 0 }} \right] = \frac{1}{2}.\frac{1}{k}\left( {\overrightarrow {AM} + \overrightarrow {BN} } \right)
\end{array}\)
Vì \(\overrightarrow {AC} = \frac{1}{k}\overrightarrow {AM} ,\overrightarrow {BD} = \frac{1}{k}\overrightarrow {BN} \), đồng thời \(\overrightarrow {AM} = \overrightarrow {AP} + \overrightarrow {PM} ,\overrightarrow {BN} = \overrightarrow {BP} + \overrightarrow {PN} \) nên \(\overrightarrow {PQ} = \frac{1}{{2k}}\left( {\overrightarrow {PM} + \overrightarrow {PN} } \right)\) (vì \(\overrightarrow {AP} + \overrightarrow {BP} = \overrightarrow 0 \))
Suy ra \(\overrightarrow {PQ} = \frac{1}{{2k}}\overrightarrow {PM} + \frac{1}{{2k}}\overrightarrow {PN} \)
Vậy ba vectơ \(\overrightarrow {PQ} ,\overrightarrow {PM} ,\overrightarrow {PN} \) đồng phẳng.
-- Mod Toán 11 HỌC247
Bài tập SGK khác
Bài tập 3.1 trang 129 SBT Hình học 11
Bài tập 3.2 trang 129 SBT Hình học 11
Bài tập 3.4 trang 130 SBT Hình học 11
Bài tập 3.5 trang 130 SBT Hình học 11
Bài tập 3.6 trang 130 SBT Hình học 11
Bài tập 3.7 trang 130 SBT Hình học 11
Bài tập 1 trang 91 SGK Hình học 11 NC
Bài tập 2 trang 91 SGK Toán 11 NC
Bài tập 3 trang 91 SGK Hình học 11 NC
Bài tập 4 trang 91 SGK Hình học 11 NC
-


Bài 1 trang 91 SGK Hình học 11
bởi thùy trang
 24/10/2018
Bài 1 (SGK trang 91)
24/10/2018
Bài 1 (SGK trang 91)Cho hình lăng trị tứ giác ABC.A'B'C'D'. Mặt phẳng (P) cắt các cạnh bên AA', BB',CC', DD' lần lượt tại I, K, L, M. Xét các vectơ có các điểm đầu là các điểm I, K, L, M và có các điểm cuối là các đỉnh của lăng trụ. Hãy chỉ ra các vectơ :
a) Cùng phương với \(\overrightarrow{IA}\)
b) Cùng hướng với \(\overrightarrow{IA}\)
c) Ngược hướng với \(\overrightarrow{IA}\)
Theo dõi (0) 1 Trả lời -


Chứng minh AD vuông góc BC biết BD vuông góc với AC và CD vuông góc với AB
bởi Nguyễn Thủy Tiên
 24/10/2018
24/10/2018
Cho tứ diện ABCD, biết BD vuông góc với AC và CD vuông góc với AB. Chứng minh rằng AD vuông góc với BC.
Theo dõi (0) 1 Trả lời