Bài tập 15 trang 28 SGK Toán 11 NC
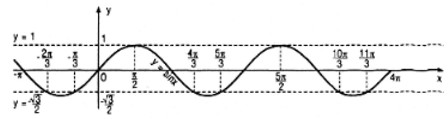
a. Vẽ đồ thị của hàm số y = sinx rồi chỉ ra trên đồ thị đó các điểm có hoành độ thuộc khoảng (−π;4π) là nghiệm của mỗi phương trình sau :
1. \(\sin x = - \frac{{\sqrt 3 }}{2}\)
2. sinx = 1
b. Cũng câu hỏi tương tự cho hàm số y = cosx đối với mỗi phương trình sau
1. \(\cos x = \frac{1}{2}\)
2. cosx = −1.
Hướng dẫn giải chi tiết
a)
\(1/\begin{array}{l}
\sin x = - \frac{{\sqrt 3 }}{2} \Leftrightarrow {\rm{sinx}} = \sin \left( { - \frac{\pi }{3}} \right)\\
\Leftrightarrow \left[ {\begin{array}{*{20}{l}}
{x = - \frac{\pi }{3} + k2\pi }\\
{x = \frac{{4\pi }}{3} + k2\pi }
\end{array}} \right.
\end{array}\)
- Với \(x = - \frac{\pi }{3} + k2\pi \) và x∈(−π;4π) ta có nghiệm:
\({x_1} = - \frac{\pi }{3},{x_2} = \frac{{5\pi }}{3},{x_3} = \frac{{11\pi }}{3}\)
- Với \(x = \frac{{4\pi }}{3} + k2\pi \) và x∈(−π;4π) ta có nghiệm:
\({x_4} = - \frac{{2\pi }}{3},{x_5} = \frac{{4\pi }}{3},{x_6} = \frac{{10\pi }}{3}\)
2/ \(\sin x = 1 \Leftrightarrow x = \frac{\pi }{2} + k2\pi \)
- Với \(x = \frac{\pi }{2} + k2\pi \) và x∈(−π;4π) ta có nghiệm :
\({x_1} = \frac{\pi }{2},{x_2} = \frac{{5\pi }}{2}\)
Xem hình vẽ
b) Tương tự câu a) ta có hình vẽ sau:
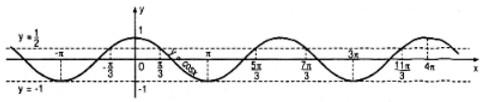
1. Nghiệm của phương trình \(\cos x = \frac{1}{2}\) thuộc khoảng (−π;4π) là:
\(\begin{array}{l}
{x_1} = - \frac{\pi }{3},{x_2} = \frac{\pi }{3},{x_3} = \frac{{5\pi }}{3},\\
{x_4} = \frac{{7\pi }}{3},{x_5} = \frac{{11\pi }}{3}
\end{array}\)
2. Nghiệm của phương trình cosx = −1 thuộc khoảng (−π;4π) là :
\({x_1} = - \pi ,{x_2} = \pi ,{x_3} = 3\pi \)
-- Mod Toán 11 HỌC247
Bài tập SGK khác
Bài tập 1.24 trang 25 SBT Toán 11
Bài tập 14 trang 28 SGK Toán 11 NC
Bài tập 16 trang 28 SGK Toán 11 NC
Bài tập 17 trang 29 SGK Toán 11 NC
Bài tập 18 trang 29 SGK Toán 11 NC
Bài tập 19 trang 29 SGK Toán 11 NC
Bài tập 20 trang 29 SGK Toán 11 NC
Bài tập 21 trang 29 SGK Toán 11 NC
Bài tập 22 trang 30 SGK Toán 11 NC
Bài tập 23 trang 31 SGK Toán 11 NC
Bài tập 24 trang 32 SGK Toán 11 NC
-


Có bao nhiêu giá trị nguyên của tham số m để phương trình cosx = m +1 có nghiệm:
bởi May May
 25/01/2021
25/01/2021
A.1
B.2
C.3
D. vô số.
Theo dõi (0) 1 Trả lời -


Số nghiệm của phương trình sin(2x – 40º) = 1 với -180º < x < 180º là:
bởi Phạm Khánh Linh
 24/01/2021
24/01/2021
A.1
B.2
C.3
D.4
Theo dõi (0) 1 Trả lời -


A. m ∈ (-∞,-1]
B. m ∈ (1,+∞]
C. m ∈ [-1,1]
D. m ≠ -1
Theo dõi (0) 1 Trả lời -


A. m ≠ 1
B. m ≠ -1
C. -1 ≤ m ≤ 1
D. m > 1
Theo dõi (0) 1 Trả lời -
ADMICRO


Giải phương trình lượng giác sau : 2sinx=cosx
bởi Khanh Linh
 05/01/2021
05/01/2021
Giai phuong trinh luong giac sau : 2sinx=cosx
Theo dõi (0) 1 Trả lời -


Giải phương trình cos2x- 3cosx4=0
bởi nguyễn huỳnh anh thư
 30/12/2020
30/12/2020
a, cos2x- 3cosx4=0
b, sin2x=sin pi/4
Theo dõi (0) 0 Trả lời -


Giải pt lượng giác (( sin^2X -1) (2|cosx| - 1))/cosx=0
bởi Nhi Nhi
 12/09/2020
Giai phuong trình (( sin^2X -1) (2|cosx| - 1))/cosx=0Theo dõi (0) 0 Trả lời
12/09/2020
Giai phuong trình (( sin^2X -1) (2|cosx| - 1))/cosx=0Theo dõi (0) 0 Trả lời -


Giải phương trình: (2cosx 1)(sin2x 2sinx-2)=4cos²x-1
bởi Phương Vũ
 10/09/2020
(2cosx 1)(sin2x 2sinx-2)=4cos²x-1Theo dõi (0) 0 Trả lời
10/09/2020
(2cosx 1)(sin2x 2sinx-2)=4cos²x-1Theo dõi (0) 0 Trả lời -


Giải phương trình: sin2x*cos(pi/5)-cos2x*sin(pi/5)=1
bởi Mạnh Cường
 06/09/2020
06/09/2020
sin2x*cos(pi/5)-cos2x*sin(pi/5)=1
Theo dõi (0) 3 Trả lời






