Bài tập 17 trang 29 SGK Toán 11 NC
Số giờ có ánh sáng mặt trời của một thành phố A ở vĩ độ 40˚ bắc trong ngày thứ t của một năm không nhuận được cho bởi hàm số
\(d\left( t \right) = 3\sin \left[ {\frac{\pi }{{182}}\left( {t - 80} \right)} \right] + 12\) với \(t \in Z,0 < t \le 365\).
a. Thành phố A có đúng 12 giờ có ánh sáng mặt trời vào ngày nào trong năm ?
b. Vào ngày nào trong năm thì thành phố A có ít giờ có ánh sáng mặt trời nhất ?
c. Vào ngày nào trong năm thì thành phố A có nhiều giờ có ánh sáng mặt trời nhất ?
Hướng dẫn giải chi tiết
a) Ta giải phương trình d(t) = 12 với t ∈ Z và 0 < t ≤ 365
Ta có:
\(\begin{array}{*{20}{l}}
\begin{array}{l}
d\left( t \right) = 12 \Leftrightarrow \sin \left[ {\frac{\pi }{{182}}\left( {t - 80} \right)} \right] = 0\\
\Leftrightarrow \frac{\pi }{{182}}\left( {t - 80} \right) = k\pi
\end{array}\\
{ \Leftrightarrow t = 182k + 80\left( {k \in Z} \right)}
\end{array}\)
Ta lại có:
\(\begin{array}{l}
0 < 182k + 80 \le 65\\
\Leftrightarrow - \frac{{80}}{{182}} < k \le \frac{{285}}{{182}} \Leftrightarrow \left[ {\begin{array}{*{20}{l}}
{k = 0}\\
{k = 1}
\end{array}} \right.
\end{array}\)
Vậy thành phố A có đúng 12 giờ ánh sáng mặt trời vào ngày thứ 80 (ứng với k = 0) và ngày thứ 262 (ứng với k = 1) trong năm.
b) Do sinx ≥ − 1 với mọi x nên thành phố A có ít giờ ánh sáng mặt trời nhất khi và chỉ khi:
\(\sin \left[ {\frac{\pi }{{182}}\left( {t - 80} \right)} \right] = - 1\) với t ∈ Z và 0 < t ≤ 365
Phương trình đó cho ta
\(\begin{array}{l}
\frac{\pi }{{182}}\left( {t - 80} \right) = - \frac{\pi }{2} + k2\pi \\
\Leftrightarrow t = 364k - 11\left( {k \in Z} \right)
\end{array}\)
Mặt khác,
\(\begin{array}{l}
0 < 364k - 11 \le 365\\
\Leftrightarrow \frac{{11}}{{364}} < k \le \frac{{376}}{{364}} \Leftrightarrow k = 1
\end{array}\)
(do k nguyên)
Vậy thành phố A có ít giờ ánh sáng mặt trời nhất (9 giờ) khi t = 353, tức là vào ngày thứ 353 trong năm.
c) Tương tự, ta phải giải phương trình:
\(\sin \left[ {\frac{\pi }{{182}}\left( {t - 80} \right)} \right] = 1\) với t ∈ Z và 0 < t ≤ 365
\(\begin{array}{*{20}{l}}
\begin{array}{l}
\frac{\pi }{{182}}\left( {t - 80} \right) = \frac{\pi }{2} + k2\pi \\
\Leftrightarrow t = 364k + 171
\end{array}\\
\begin{array}{l}
0 < 364k + 171 \le 365\\
\Leftrightarrow - \frac{{171}}{{364}} < k \le \frac{{194}}{{364}} \Leftrightarrow k = 0
\end{array}
\end{array}\)
Vậy thành phố A có nhiều giờ có ánh sáng mặt trời nhất (15 giờ) vào ngày thứ 171 trong năm.
-- Mod Toán 11 HỌC247
Bài tập SGK khác
Bài tập 15 trang 28 SGK Toán 11 NC
Bài tập 16 trang 28 SGK Toán 11 NC
Bài tập 18 trang 29 SGK Toán 11 NC
Bài tập 19 trang 29 SGK Toán 11 NC
Bài tập 20 trang 29 SGK Toán 11 NC
Bài tập 21 trang 29 SGK Toán 11 NC
Bài tập 22 trang 30 SGK Toán 11 NC
Bài tập 23 trang 31 SGK Toán 11 NC
Bài tập 24 trang 32 SGK Toán 11 NC
-


Giải phương trình Cos(x +π/18)=2/5tan(2x-1)=√3
bởi Ngọc Bảo
 11/08/2020
Theo dõi (0) 0 Trả lời
11/08/2020
Theo dõi (0) 0 Trả lời -


Giải phương trình 3sin3x -4cos3x =5
bởi Trần Thị Phương Thảo
 03/08/2020
3sin3x -4cos3x =5Theo dõi (2) 3 Trả lời
03/08/2020
3sin3x -4cos3x =5Theo dõi (2) 3 Trả lời -

 Theo dõi (1) 1 Trả lời
Theo dõi (1) 1 Trả lời -


Help me >< thank you
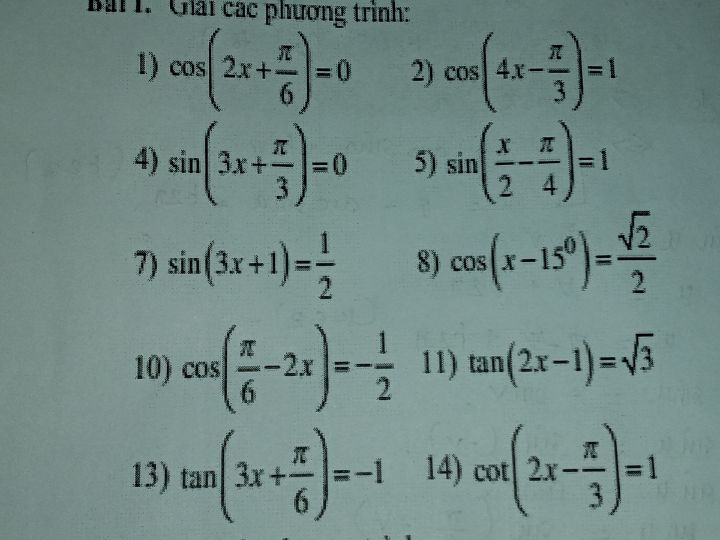 Theo dõi (0) 1 Trả lời
Theo dõi (0) 1 Trả lời -
ADMICRO


Giải phương trình \(\tan 2x . \tan x =1\)?
bởi Thiên Lý
 30/07/2020
30/07/2020
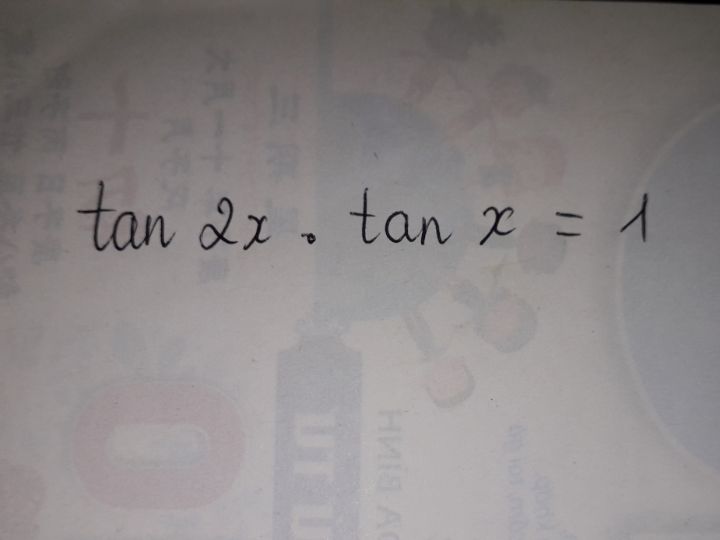 Theo dõi (0) 1 Trả lời
Theo dõi (0) 1 Trả lời -


Giải phương trình \({\cot ^4}x - 4{\cot ^2}x + 3 = 0\)?
bởi Hằng
 30/07/2020
30/07/2020
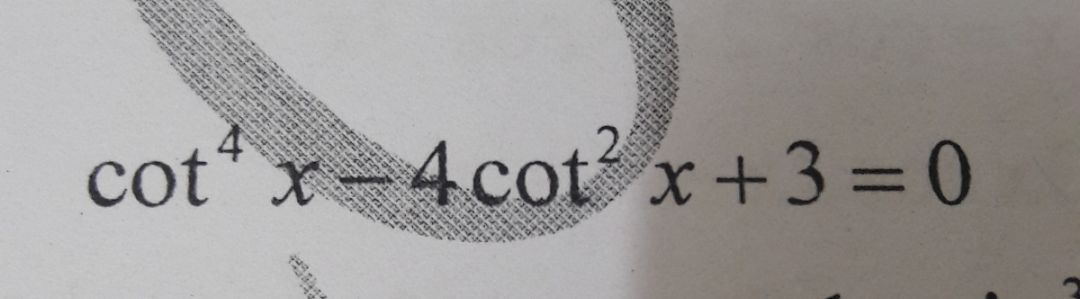 Theo dõi (0) 0 Trả lời
Theo dõi (0) 0 Trả lời -


giúp mk tìm x vs ạ
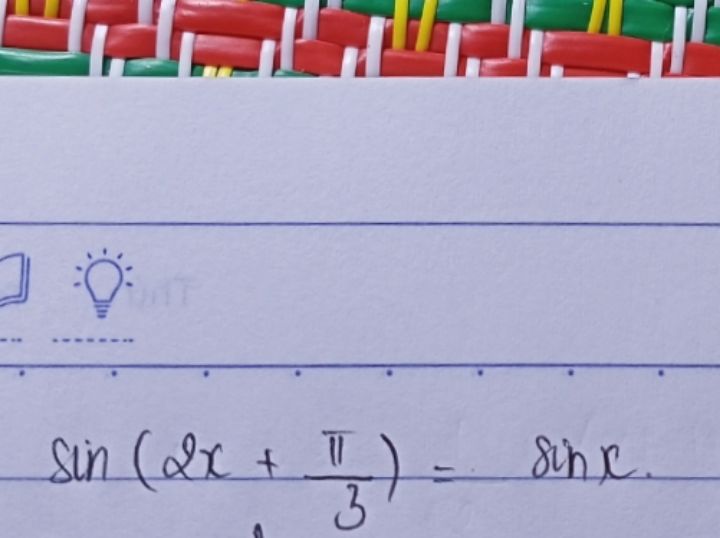 Theo dõi (0) 1 Trả lời
Theo dõi (0) 1 Trả lời -


Giải phương trình: 2cosx.cos2x=1+sin2x.sinx?
bởi Hitori Miko
 21/07/2020
21/07/2020
2cosx.cos2x=1+sin2x.sĩn
Theo dõi (0) 1 Trả lời -


Giải phương trình \(\sin \left( {2x + \frac{\pi }{6}} \right) = \frac{{ - \sqrt 2 }}{2}\)?
bởi Vũ Hoàng Hương Giang
 19/07/2020
19/07/2020
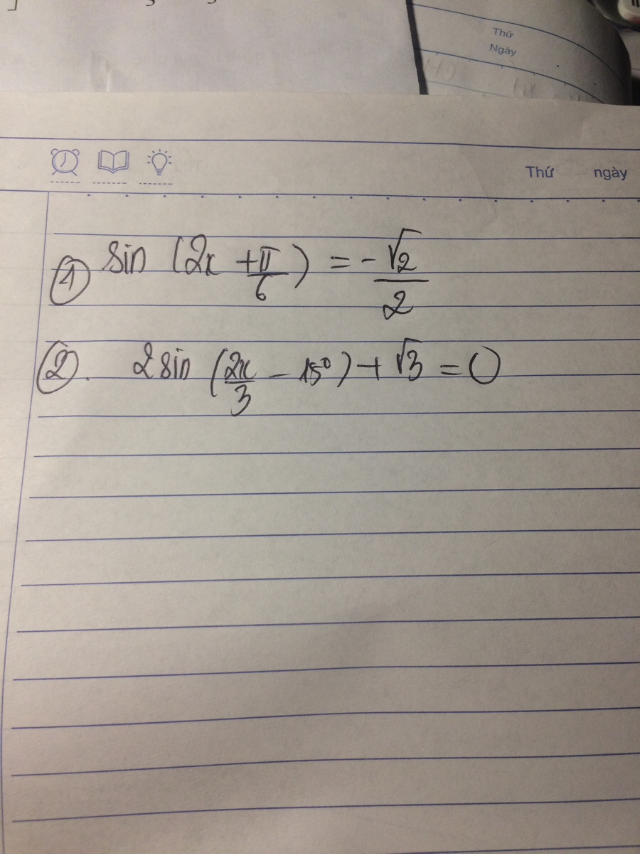 Theo dõi (0) 1 Trả lời
Theo dõi (0) 1 Trả lời





