Các em ơi, biết đâu đấy, việc tóm tắt kiến thức sau mỗi bài học lại giống như việc chế biến món ăn trước mỗi bữa ăn. Đó chính là cách nhanh chóng và hiệu quả cho hệ thống kiến thức đấy.
Ở HOC247, có bộ Tóm tắt lý thuyết về bài Hàm số liên tục trong sách Chân trời sáng tạo lớp 11. Đặc biệt, các em còn có thể tham khảo ngay cả bài tập minh họa sau bài học luôn. Có quá tuyệt phải không? Điều này giúp các em có một công cụ, phương pháp giải các dạng toán liên quan đến hàm số liên tục. Vì vậy, hãy học tập với tinh thần cao cả và cố gắng tận hưởng quá trình học tập. Các em chắc chắn sẽ đạt được kết quả tuyệt vời.
Tóm tắt lý thuyết
1.1. Hàm số liên tục tại một điểm
|
Cho hàm số \(y = f(x)\) xác định trên khoảng K và \({x_0} \in K\). - Hàm số \(y = f(x)\) được gọi là liên tục tại điểm \({x_0} \Leftrightarrow \mathop {\lim }\limits_{x \to {x_0}} f(x) = f({x_0})\). |
Nhận xét: Để hàm số \(y = f(x)\) liên tục tại \({x_0}\) thì phải có cả ba điều sau:
1. Hàm số xác định tại \({x_0}\)
2. Tồn tại \(\mathop {\lim }\limits_{x \to {x_0}} f(x)\).
3. \(\mathop {\lim }\limits_{x \to {x_0}} f(x) = f({x_0})\).
Chú ý: Khi hàm số \(y = f(x)\) không liên tục tại điểm \({x_0}\) thì ta nói \(y = f(x)\) gián đoạn tại điểm \({x_0}\) và \({x_0}\) được gọi là điểm gián đoạn của hàm số f(x).
1.2. Hàm số liên tục trên một khoảng, trên một đoạn
|
Cho hàm số \(y = f(x)\) xác định trên khoảng (a;b). - \(y = f(x)\) được gọi là liên tục trên một khoảng nếu nó kiên tục tại mọi điểm của khoảng đó. - \(y = f(x)\) được gọi là liên tục trên đoạn \(\left[ {a;b} \right]\) nếu nó liên tục trên \(\left( {a;b} \right)\) và \(\mathop {\lim }\limits_{x \to {a^ + }} f(x) = f(a)\), \(\mathop {\lim }\limits_{x \to {b^ - }} f(x) = f(b)\). |
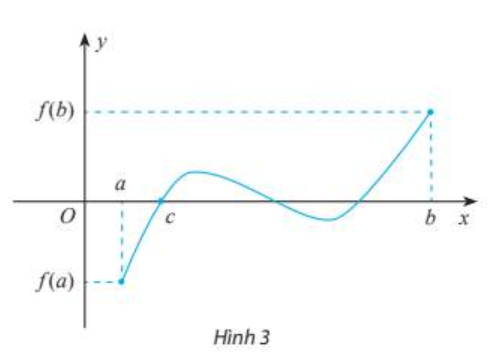
Nhận xét: Đồ thị của hàm số y=f(x) liên tục trên đoạn [a; b] là một đường liền, có điểm đẩu, điểm cuối (Hình 3).
Nếu hai điểm này nằm về hai phía so với trục hoành thì đường liền nói trên luôn cắt trục hoành tại ít nhất một điểm. Điều này có thể được phát biểu dưới dạng như sau: Nếu hàm số y= f (x) liên tục trên đoạn [a, b] và f (a).f (b)< 0 thì luôn tồn tại ít nhất một điểm \(c \in (a, b)\) sao cho f(c)=0.
1.3. Tính liên tục của hàm số sơ cấp
- Hàm số đa thức \(y = P(x)\) và các hàm số lượng giác \(y = \sin x, y=\cos x\) liên tục trên R.
- Hàm số phân thức \(y = {P(x)\over Q(x)}\), hàm số căn thức \(y = \sqrt f(x)\) và hàm số lượng giác \(y = \tan x, y=\cot x\) liên tục trên các khoảng xác định của chúng.
Trong đó P(x) và Q(x) là các đa thức.
Nhận xét: Hàm số thuộc những loại trên được gọi chung là hàm số sơ cấp.
1.4. Tổng, hiệu, tích, thương của hàm số liên tục
Các hàm số \(y = f(x),{\rm{ }}y = g(x)\) liên tục tại \({x_0}\). Khi đó tổng, hiệu, tích liên tục tại x0, thương \(y = \frac{{f(x)}}{{g(x)}}\) liên tục tại x0 nếu \(g({x_0}) \ne 0\).
Bài tập minh họa
Câu 1. Cho hàm số \(f(x)=\frac{2x+3}{x-2}\). Mệnh đề nào sau đây đúng?
A. Hàm số liên tục trên khoảng \(\left( 1;5 \right)\).
B. Hàm số gián đoạn tại \(x=2020\).
C. Hàm số liên tục tại \(x=2\).
D. Hàm số gián đoạn tại \(x=2\).
Hướng dẫn giải
Chọn D
Vì hàm số không tồn tại f(2) nên hàm số bị gián đoạn tại \(x=2\)
Câu 2. Hàm số nào sau đây không liên tục tại\(x=2\)
A. \(y=\sqrt{x+2}\).
B. \(y=\sin x\).
C. \(y=\frac{{{x}^{2}}}{x-2}\).
D. \(y={{x}^{2}}-3x+2\).
Hướng dẫn giải
Chọn C
Hàm số \(y=\frac{{{x}^{2}}}{x-2}\) không xác định tại \(x=2\) nên không liên tục tại \(x=2\).
Luyện tập Bài 3 Toán 11 Chân Trời Sáng Tạo
Học xong bài học này, em có thể:
- Nhận dạng được hàm số liên tục tại một điểm, hoặc trên một khoảng, hoặc trên một đoạn.
- Nhận biết tính liên tục của tổng, hiệu, tích, thương của hai hàm số liên tục, tỉnh liên tục của một số hàm số sơ cấp cơ bản.
3.1. Trắc nghiệm Bài 3 Toán 11 Chân Trời Sáng Tạo
Các em có thể hệ thống lại nội dung kiến thức đã học được thông qua bài kiểm tra Trắc nghiệm Toán 11 Chân trời sáng tạo Chương 3 Bài 3 cực hay có đáp án và lời giải chi tiết.
-
- A. Hàm số liên tục trên khoảng \(\left( 1;5 \right)\).
- B. Hàm số gián đoạn tại \(x=2020\).
- C. Hàm số liên tục tại \(x=2\).
- D. Hàm số gián đoạn tại \(x=2\).
-
- A. \(-\frac{1}{2}\).
- B. \(\frac{1}{5}\).
- C. \(\frac{1}{3}\).
- D. \(\frac{1}{4}\).
-
- A. \(y=\sqrt{x+2}\).
- B. \(y=\sin x\).
- C. \(y=\frac{{{x}^{2}}}{x-2}\).
- D. \(y={{x}^{2}}-3x+2\).
Câu 4-10: Mời các em đăng nhập xem tiếp nội dung và thi thử Online để củng cố kiến thức về bài học này nhé!
3.2. Bài tập SGK Bài 3 Toán 11 Chân Trời Sáng Tạo
Các em có thể xem thêm phần hướng dẫn Giải bài tập Toán 11 Chân trời sáng tạo Chương 3 Bài 3 để giúp các em nắm vững bài học và các phương pháp giải bài tập.
Hoạt động khởi động trang 80 SGK Toán 11 Chân trời sáng tạo tập 1 - CTST
Hoạt động khám phá 1 trang 80 SGK Toán 11 Chân trời sáng tạo tập 1 - CTST
Thực hành 1 trang 81 SGK Toán 11 Chân trời sáng tạo tập 1 - CTST
Hoạt động khám phá 2 trang 82 SGK Toán 11 Chân trời sáng tạo tập 1 - CTST
Vận dụng 1 trang 82 SGK Toán 11 Chân trời sáng tạo tập 1 - CTST
Thực hành 2 trang 82 SGK Toán 11 Chân trời sáng tạo tập 1 - CTST
Hoạt động khám phá 3 trang 82 SGK Toán 11 Chân trời sáng tạo tập 1 - CTST
Thực hành 3 trang 83 SGK Toán 11 Chân trời sáng tạo tập 1 - CTST
Thực hành 4 trang 83 SGK Toán 11 Chân trời sáng tạo tập 1 - CTST
Vận dụng 2 trang 83 SGK Toán 11 Chân trời sáng tạo tập 1 - CTST
Hoạt động khám phá 4 trang 83 SGK Toán 11 Chân trời sáng tạo tập 1 - CTST
Thực hành 5 trang 84 SGK Toán 11 Chân trời sáng tạo tập 1 - CTST
Vận dụng 3 trang 84 SGK Toán 11 Chân trời sáng tạo tập 1 - CTST
Giải Bài 1 trang 84 SGK Toán 11 Chân trời sáng tạo tập 1 - CTST
Giải Bài 2 trang 84 SGK Toán 11 Chân trời sáng tạo tập 1 - CTST
Giải Bài 3 trang 85 SGK Toán 11 Chân trời sáng tạo tập 1 - CTST
Giải Bài 4 trang 85 SGK Toán 11 Chân trời sáng tạo tập 1 - CTST
Giải Bài 5 trang 85 SGK Toán 11 Chân trời sáng tạo tập 1 - CTST
Giải Bài 6 trang 85 SGK Toán 11 Chân trời sáng tạo tập 1 - CTST
Bài tập 1 trang 90 SBT Toán 11 Tập 1 Chân trời sáng tạo - CTST
Bài tập 2 trang 90 SBT Toán 11 Tập 1 Chân trời sáng tạo - CTST
Bài tập 3 trang 90 SBT Toán 11 Tập 1 Chân trời sáng tạo - CTST
Bài tập 4 trang 90 SBT Toán 11 Tập 1 Chân trời sáng tạo - CTST
Bài tập 5 trang 90 SBT Toán 11 Tập 1 Chân trời sáng tạo - CTST
Bài tập 6 trang 90 SBT Toán 11 Tập 1 Chân trời sáng tạo - CTST
Bài tập 7 trang 90 SBT Toán 11 Tập 1 Chân trời sáng tạo - CTST
Bài tập 8 trang 91 SBT Toán 11 Tập 1 Chân trời sáng tạo - CTST
Bài tập 9 trang 91 SBT Toán 11 Tập 1 Chân trời sáng tạo - CTST
Bài tập 10 trang 91 SBT Toán 11 Tập 1 Chân trời sáng tạo - CTST
Bài tập 11 trang 91 SBT Toán 11 Tập 1 Chân trời sáng tạo - CTST
Bài tập 12 trang 91 SBT Toán 11 Tập 1 Chân trời sáng tạo - CTST
Hỏi đáp Bài 3 Toán 11 Chân Trời Sáng Tạo
Trong quá trình học tập nếu có thắc mắc hay cần trợ giúp gì thì các em hãy comment ở mục Hỏi đáp, Cộng đồng Toán học HOC247 sẽ hỗ trợ cho các em một cách nhanh chóng!
Chúc các em học tập tốt và luôn đạt thành tích cao trong học tập!
-- Mod Toán Học 11 HỌC247