Bà i háŧc "LÅĐy tháŧŦa váŧi sáŧ mÅĐ tháŧąc" trong chÆ°ÆĄng trÃŽnh ToÃĄn 11 - Kášŋt náŧi tri tháŧĐc là máŧt phᚧn trong chÆ°ÆĄng trÃŽnh háŧc váŧ hà m sáŧ. Trong bà i háŧc nà y, cÃĄc em sáš― ÄÆ°áŧĢc giášĢi thÃch váŧ cÃĄc khÃĄi niáŧm cÆĄ bášĢn cáŧ§a lÅĐy tháŧŦa và sáŧ mÅĐ, cÅĐng nhÆ° cÃĄch tÃnh toÃĄn vÃ ÃĄp dáŧĨng chÚng trong tháŧąc tášŋ. Ngoà i ra, bà i háŧc cÅĐng Äáŧ cášp Äášŋn cÃĄc tÃnh chášĨt cáŧ§a lÅĐy tháŧŦa váŧi sáŧ mÅĐ tháŧąc, bao gáŧm cášĢ phÃĐp nhÃĒn, phÃĐp chia, và cÃĄch Äáŧi cÆĄ sáŧ. Cuáŧi cÃđng, bà i giášĢng sáš― ÄÆ°a ra máŧt sáŧ và dáŧĨ tháŧąc tášŋ váŧ áŧĐng dáŧĨng cáŧ§a lÅĐy tháŧŦa váŧi sáŧ mÅĐ tháŧąc, giÚp cÃĄc em hiáŧu rÃĩ hÆĄn váŧ tᚧm quan tráŧng cáŧ§a chÚng trong cuáŧc sáŧng hà ng ngà y.
TÃģm tášŊt lÃ― thuyášŋt
1.1. LÅĐy tháŧŦa váŧi sáŧ mÅĐ nguyÊn
a) LÅĐy tháŧŦa váŧi sáŧ mÅĐ nguyÊn
- Cho n là máŧt sáŧ nguyÊn dÆ°ÆĄng. Ta Äáŧnh nghÄĐa:
+ Váŧi a là sáŧ tháŧąc tuáŧģ Ã―:
\[a^n = \underbrace{a\cdot a\cdots a}_{n\text{ tháŧŦa sáŧ}}.\]
+ Váŧi a là sáŧ tháŧąc khÃĄc 0.
\[a^0 = 1; a ^{-n} = {1\over a^n}.\]
- Trong biáŧu tháŧĐc \(a^m\), a gáŧi là cÆĄ sáŧ, m gáŧi là sáŧ mÅĐ.
ChÚ Ã―: \(0^0\) và \(0^{-n} (n \in N)\) khÃīng cÃģ nghÄĐa.
b) TÃnh chášĨt
Luáŧđ tháŧŦa váŧi sáŧ mÅĐ nguyÊn cÃģ cÃĄc tÃnh chášĨt tÆ°ÆĄng táŧą nhÆ° luáŧđ tháŧŦa váŧi sáŧ mÅĐ nguyÊn dÆ°ÆĄng.
|
Váŧi \(a \ne 0, b \ne 0\) và m, n là cÃĄc sáŧ nguyÊn, ta cÃģ: \(\begin{array}{l} {a^m}.{a^n} = {a^{m + n}};{\quad\quad\quad}\frac{{{a^m}}}{{{a^n}}} = {a^{m - n}};\\ {\left( {{a^m}} \right)^n} = {a^{mn}};{\quad\quad\quad}{\left( {ab} \right)^m} = {a^m}{b^m};\\ {\left( {\frac{a}{b}} \right)^m} = \frac{{{a^m}}}{{{b^m}}}. \end{array}\) |
ChÚ Ã―:
+ Nášŋu a > 1 thÃŽ \(a^m >a^n\) khi và cháŧ khi m > n.
+ Nášŋu 0 < a < 1 thÃŽ \(a^m >a^n\) khi và cháŧ khi m < n.
1.2. LÅĐy tháŧŦa váŧi sáŧ mÅĐ háŧŊu táŧ
a) KhÃĄi niáŧm cÄn bášc n
|
Cho sáŧ tháŧąc a và sáŧ nguyÊn dÆ°ÆĄng n. Sáŧ b ÄÆ°áŧĢc gáŧi là cÄn bášc n cáŧ§a sáŧ a nášŋu \(b^n = a\). |
Nhášn xÃĐt: + Khi n là sáŧ lášŧ, máŧi sáŧ tháŧąc a cháŧ cÃģ máŧt cÄn bášc n và kà hiáŧu là \(\sqrt[n]{a}\). CÄn bášc 1 cáŧ§a sáŧ a chÃnh là a.
+ Khi n là sáŧ chášĩn, máŧi sáŧ tháŧąc dÆ°ÆĄng cÃģ ÄÚng hai cÄn bášc n là hai sáŧ Äáŧi nhau, giášĢ tráŧ dÆ°ÆĄng kà hiáŧu là \(\sqrt[n]{a} \) (gáŧi là cÄn sáŧ háŧc bášc n cáŧ§a a), giÃĄ tráŧ ÃĒm kà hiáŧu là \(-\sqrt[n]{a} \).
b) TÃnh chášĨt cáŧ§a cÄn bášc n
GiášĢ sáŧ n, k là cÃĄc sáŧ nguyÊn dÆ°ÆĄng, m là sáŧ nguyÊn. Khi ÄÃģ:
(GiášĢ thiášŋt cÃĄc biáŧu tháŧĐc áŧ trÊn Äáŧu cÃģ nghÄĐa).
c) LÅĐy tháŧŦa váŧi sáŧ mÅĐ háŧŊu táŧ
|
Cho sáŧ tháŧąc a dÆ°ÆĄng và sáŧ háŧŊu táŧ \(r = \frac{m}{n}\) trong ÄÃģ m là máŧt sáŧ nguyÊn và n là sáŧ nguyÊn dÆ°ÆĄng. Luáŧđ tháŧŦa cáŧ§a a váŧi sáŧ mÅĐ r, kà hiáŧu là \(a^r\), xÃĄc Äáŧnh báŧi \[{a^r} = {a^{\frac{m}{n}}} = \sqrt[n]{{{a^m}}}.\] |
ChÚ Ã―: Luáŧđ tháŧŦa váŧi sáŧ mÅĐ háŧŊu táŧ (cáŧ§a máŧt sáŧ tháŧąc dÆ°ÆĄng) cÃģ Äᚧy Äáŧ§ cÃĄc tÃnh chášĨt nhÆ° luáŧđ tháŧŦa váŧi sáŧ mÅĐ nguyÊn ÄÃĢ nÊu trong MáŧĨc 1.

1.3. LÅĐy tháŧŦa váŧi sáŧ mÅĐ tháŧąc
a) KhÃĄi niáŧm lÅĐy tháŧŦa váŧi sáŧ mÅĐ tháŧąc
|
Cho a là sáŧ tháŧąc dÆ°ÆĄng và \(\alpha\) là máŧt sáŧ vÃī táŧ. XÃĐt dÃĢy sáŧ háŧŊu táŧ (\(r_n\) ) mà \(\mathop {\lim }\limits_{n \to + \infty } {r_n} = \alpha \). Luáŧđ tháŧŦa cáŧ§a a váŧi sáŧ mÅĐ \(\alpha\), kà hiáŧu là \(a^\alpha\). \[{a^\alpha } = \mathop {\lim }\limits_{n \to + \infty } {a^{{r_n}}}.\] |
ChÚ Ã―: Luáŧđ tháŧŦa váŧi sáŧ mÅĐ tháŧąc (cáŧ§a máŧt sáŧ dÆ°ÆĄng) cÃģ Äᚧy Äáŧ§ cÃĄc tÃnh chášĨt nhÆ° luáŧđ tháŧŦa váŧi sáŧ mÅĐ nguyÊn ÄÃĢ nÊu trong MáŧĨc 1.
b) TÃnh lÅĐy tháŧŦa váŧi sáŧ mÅĐ tháŧąc bášąng mÃĄy tÃnh cᚧm tay
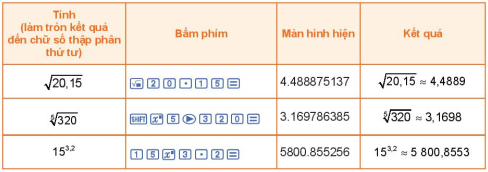
BÃ i tášp minh háŧa
VÃ dáŧĨ 1:
RÚt gáŧn biáŧu tháŧĐc: \(A = \frac{{{a^{ - n}} + {b^{ - n}}}}{{{a^{ - n}} - {b^{ - n}}}} - \frac{{{a^{ - n}} - {b^{ - n}}}}{{{a^{ - n}} + {b^{ - n}}}}\left( {ab \ne 0;a \ne \pm b} \right)\).
HÆ°áŧng dášŦn giášĢi
\(A = \frac{{{a^{ - n}} + {b^{ - n}}}}{{{a^{ - n}} - {b^{ - n}}}} - \frac{{{a^{ - n}} - {b^{ - n}}}}{{{a^{ - n}} + {b^{ - n}}}} = \frac{{{a^n} + {b^n}}}{{{a^n}{b^n}\left( {\frac{{{b^n} - {a^n}}}{{{a^n}{b^n}}}} \right)}} - \frac{{{b^n} - {a^n}}}{{{a^n}{b^n}\left( {\frac{{{a^n} + {b^n}}}{{{a^n}{b^n}}}} \right)}}\).
\(= \frac{{{{\left( {{a^n} + {b^n}} \right)}^2} - {{\left( {{b^n} - {a^n}} \right)}^2}}}{{\left( {{a^n} + {b^n}} \right)\left( {{b^n} - {a^n}} \right)}} = \frac{{4{a^n}{b^n}}}{{{b^{2n}} - {a^{2n}}}}\).
VÃ dáŧĨ 2:
Cho a,b là cÃĄc sáŧ tháŧąc dÆ°ÆĄng .RÚt gáŧn biáŧu tháŧĐc sau:
a) \(\left( {1 - 2\sqrt {\frac{a}{b}} + \frac{b}{a}} \right):{\left( {{a^{\frac{1}{2}}} - {b^{\frac{1}{2}}}} \right)^2}\).
b) \(\frac{{{a^{\frac{1}{4}}} - {a^{\frac{9}{4}}}}}{{{a^{\frac{1}{4}}} - {a^{\frac{5}{4}}}}} - \frac{{{b^{ - \frac{1}{2}}} - {b^{\frac{3}{2}}}}}{{{b^{\frac{1}{2}}} + {b^{ - \frac{1}{2}}}}}\).
HÆ°áŧng dášŦn giášĢi
a) \(\left( {1 - 2\sqrt {\frac{a}{b}} + \frac{b}{a}} \right):{\left( {{a^{\frac{1}{2}}} - {b^{\frac{1}{2}}}} \right)^2} = {\left( {1 - \sqrt {\frac{a}{b}} } \right)^2}:\left( {\sqrt a - \sqrt b } \right)\).
\(= \frac{{{{\left( {\sqrt b - \sqrt a } \right)}^2}}}{b}.\frac{1}{{{{\left( {\sqrt a - \sqrt b } \right)}^2}}} = \frac{1}{b}\)
b) \(\frac{{{a^{\frac{1}{4}}} - {a^{\frac{9}{4}}}}}{{{a^{\frac{1}{4}}} - {a^{\frac{5}{4}}}}} - \frac{{{b^{ - \frac{1}{2}}} - {b^{\frac{3}{2}}}}}{{{b^{\frac{1}{2}}} + {b^{ - \frac{1}{2}}}}} = \frac{{{a^{\frac{1}{4}}}\left( {1 - {a^2}} \right)}}{{{a^{\frac{1}{4}}}\left( {1 - a} \right)}} - \frac{{{b^{ - \frac{1}{2}}}\left( {1 - {b^2}} \right)}}{{{b^{ - \frac{1}{2}}}\left( {{b^2} - 1} \right)}} = 1 + a + 1 = a + 2\).
Luyáŧn tášp BÃ i 18 ToÃĄn 11 Kášŋt Náŧi Tri TháŧĐc
Háŧc xong bà i háŧc nà y, em cÃģ tháŧ:
- Nhášn biášŋt khÃĄi niáŧm luáŧđ tháŧŦa váŧi sáŧ mÅĐ nguyÊn khÃĄc 0; sáŧ mÅĐ háŧŊu táŧ và sáŧ mÅĐ tháŧąc cáŧ§a máŧt sáŧ tháŧąc dÆ°ÆĄng. GiášĢi thÃch tÃnh chášĨt cáŧ§a luáŧđ tháŧŦa váŧi sáŧ mÅĐ nguyÊn, luáŧđ tháŧŦa váŧi sáŧ mÅĐ háŧŊu táŧ và luáŧđ tháŧŦa váŧi sáŧ mÅĐ tháŧąc.
- Sáŧ dáŧĨng tÃnh chášĨt cáŧ§a phÃĐp tÃnh luáŧđ tháŧŦa trong tÃnh toÃĄn. TÃnh giÃĄ tráŧ biáŧu tháŧĐc bášąng mÃĄy tÃnh cᚧm tay. GiášĢi quyášŋt máŧt sáŧ vášĨn Äáŧ tháŧąc tiáŧ n gášŊn váŧi phÃĐp tÃnh luáŧđ tháŧŦa.
3.1. TrášŊc nghiáŧm BÃ i 18 ToÃĄn 11 Kášŋt Náŧi Tri TháŧĐc
CÃĄc em cÃģ tháŧ háŧ tháŧng lᚥi náŧi dung kiášŋn tháŧĐc ÄÃĢ háŧc ÄÆ°áŧĢc thÃīng qua bà i kiáŧm tra TrášŊc nghiáŧm ToÃĄn 11 Kášŋt náŧi tri tháŧĐc ChÆ°ÆĄng 6 Bà i 18 cáŧąc hay cÃģ ÄÃĄp ÃĄn và láŧi giášĢi chi tiášŋt.
-
- A. 1
- B. \(\frac{1}{{16}}\)
- C. \(1\frac{3}{{16}}\)
- D. \(\frac{7}{{8}}\)
-
- A. an
- B. na
- C. na
- D. a + n
-
CÃĒu 3:
Cho sáŧ nguyÊn dÆ°ÆĄng nâĨ2, sáŧ a ÄÆ°áŧĢc gáŧi là cÄn bášc n cáŧ§a sáŧ tháŧąc b nášŋu:
- A. bn=a
- B. an=b
- C. an=bn
- D. na=b
CÃĒu 4-10: Máŧi cÃĄc em ÄÄng nhášp xem tiášŋp náŧi dung và thi tháŧ Online Äáŧ cáŧ§ng cáŧ kiášŋn tháŧĐc váŧ bà i háŧc nà y nhÃĐ!
3.2. BÃ i tášp SGK BÃ i 18 ToÃĄn 11 Kášŋt Náŧi Tri TháŧĐc
CÃĄc em cÃģ tháŧ xem thÊm phᚧn hÆ°áŧng dášŦn GiášĢi bà i tášp ToÃĄn 11 Kášŋt náŧi tri tháŧĐc ChÆ°ÆĄng 6 Bà i 18 Äáŧ giÚp cÃĄc em nášŊm váŧŊng bà i háŧc và cÃĄc phÆ°ÆĄng phÃĄp giášĢi bà i tášp.
Hoᚥt Äáŧng 1 trang 5 SGK ToÃĄn 11 KÊĖt nÃīĖi tri thÆ°Ėc tášp 2 - KNTT
Luyáŧn tášp 1 trang 5 SGK ToÃĄn 11 KÊĖt nÃīĖi tri thÆ°Ėc tášp 2 - KNTT
Hoᚥt Äáŧng 2 trang 6 SGK ToÃĄn 11 KÊĖt nÃīĖi tri thÆ°Ėc tášp 2 - KNTT
Luyáŧn tášp 2 trang 6 SGK ToÃĄn 11 KÊĖt nÃīĖi tri thÆ°Ėc tášp 2 - KNTT
Hoᚥt Äáŧng 3 trang 6 SGK ToÃĄn 11 KÊĖt nÃīĖi tri thÆ°Ėc tášp 2 - KNTT
Luyáŧn tášp 3 trang 7 SGK ToÃĄn 11 KÊĖt nÃīĖi tri thÆ°Ėc tášp 2 - KNTT
Luyáŧn tášp 4 trang 7 SGK ToÃĄn 11 KÊĖt nÃīĖi tri thÆ°Ėc tášp 2 - KNTT
Hoᚥt Äáŧng 5 trang 7 SGK ToÃĄn 11 KÊĖt nÃīĖi tri thÆ°Ėc tášp 2 - KNTT
Luyáŧn tášp 5 trang 8 SGK ToÃĄn 11 KÊĖt nÃīĖi tri thÆ°Ėc tášp 2 - KNTT
Vášn dáŧĨng trang 8 SGK ToÃĄn 11 KÊĖt nÃīĖi tri thÆ°Ėc tášp 2 - KNTT
GiášĢi Bà i 6.1 trang 9 SGK ToÃĄn 11 KÊĖt nÃīĖi tri thÆ°Ėc tášp 2 - KNTT
GiášĢi Bà i 6.2 trang 9 SGK ToÃĄn 11 KÊĖt nÃīĖi tri thÆ°Ėc tášp 2 - KNTT
GiášĢi Bà i 6.3 trang 9 SGK ToÃĄn 11 KÊĖt nÃīĖi tri thÆ°Ėc tášp 2 - KNTT
GiášĢi Bà i 6.4 trang 9 SGK ToÃĄn 11 KÊĖt nÃīĖi tri thÆ°Ėc tášp 2 - KNTT
GiášĢi Bà i 6.5 trang 9 SGK ToÃĄn 11 KÊĖt nÃīĖi tri thÆ°Ėc tášp 2 - KNTT
GiášĢi Bà i 6.6 trang 9 SGK ToÃĄn 11 KÊĖt nÃīĖi tri thÆ°Ėc tášp 2 - KNTT
GiášĢi Bà i 6.7 trang 9 SGK ToÃĄn 11 KÊĖt nÃīĖi tri thÆ°Ėc tášp 2 - KNTT
GiášĢi Bà i 6.8 trang 9 SGK ToÃĄn 11 KÊĖt nÃīĖi tri thÆ°Ėc tášp 2 - KNTT
BaĖi tÃĒĖĢp 6.1 trang 6 SBT ToaĖn 11 TÃĒĖĢp 2 KÊĖt nÃīĖi tri thÆ°Ėc - KNTT
BaĖi tÃĒĖĢp 6.2 trang 6 SBT ToaĖn 11 TÃĒĖĢp 2 KÊĖt nÃīĖi tri thÆ°Ėc - KNTT
BaĖi tÃĒĖĢp 6.3 trang 6 SBT ToaĖn 11 TÃĒĖĢp 2 KÊĖt nÃīĖi tri thÆ°Ėc - KNTT
BaĖi tÃĒĖĢp 6.4 trang 6 SBT ToaĖn 11 TÃĒĖĢp 2 KÊĖt nÃīĖi tri thÆ°Ėc - KNTT
BaĖi tÃĒĖĢp 6.5 trang 6 SBT ToaĖn 11 TÃĒĖĢp 2 KÊĖt nÃīĖi tri thÆ°Ėc - KNTT
BaĖi tÃĒĖĢp 6.6 trang 7 SBT ToaĖn 11 TÃĒĖĢp 2 KÊĖt nÃīĖi tri thÆ°Ėc - KNTT
BaĖi tÃĒĖĢp 6.7 trang 7 SBT ToaĖn 11 TÃĒĖĢp 2 KÊĖt nÃīĖi tri thÆ°Ėc - KNTT
BaĖi tÃĒĖĢp 6.8 trang 7 SBT ToaĖn 11 TÃĒĖĢp 2 KÊĖt nÃīĖi tri thÆ°Ėc - KNTT
BaĖi tÃĒĖĢp 6.9 trang 7 SBT ToaĖn 11 TÃĒĖĢp 2 KÊĖt nÃīĖi tri thÆ°Ėc - KNTT
BaĖi tÃĒĖĢp 6.10 trang 7 SBT ToaĖn 11 TÃĒĖĢp 2 KÊĖt nÃīĖi tri thÆ°Ėc - KNTT
Háŧi ÄÃĄp BÃ i 18 ToÃĄn 11 Kášŋt Náŧi Tri TháŧĐc
Trong quÃĄ trÃŽnh háŧc tášp nášŋu cÃģ thášŊc mášŊc hay cᚧn tráŧĢ giÚp gÃŽ thÃŽ cÃĄc em hÃĢy comment áŧ máŧĨc Háŧi ÄÃĄp, Cáŧng Äáŧng ToÃĄn háŧc HOC247 sáš― háŧ tráŧĢ cho cÃĄc em máŧt cÃĄch nhanh chÃģng!
ChÚc cÃĄc em háŧc tášp táŧt và luÃīn Äᚥt thà nh tÃch cao trong háŧc tášp!
-- Mod ToÃĄn Háŧc 11 HáŧC247










