Giải bài 3 trang 81 SBT Toán 10 Chân trời sáng tạo tập 1
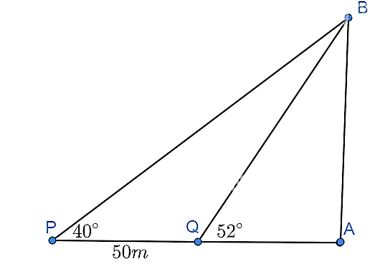
Hai chiếc tàu thủy P và Q cách nhau 50 m. Từ P và Q thẳng hàng với chân A của tháp hải đăng AB ở trên bờ biển, người ta nhìn chiều cao AB của tháp dưới các góc \(\widehat {BPA} = 40^\circ \) và \(\widehat {BQA} = 52^\circ \). Tính chiều cao của tháp hải đăng đó.
Hướng dẫn giải chi tiết Bài 3
Phương pháp giải
Áp dụng định lí sin
Trong tam giác ABC với BC = a, CA = b, AB = c, ta có:
\(\frac{a}{{\sin A}} = \frac{b}{{\sin B}} = \frac{c}{{\sin C}} = 2R.\)
Lời giải chi tiết
Góc \(\widehat {PQB}\) là góc bù của tam giác BPQ nên ta có:
\(\widehat {BQP} = \widehat {QPB} + \widehat {PBQ} \Rightarrow \widehat {PBQ} = \widehat {BQP} - \widehat {QPB} = 52^\circ - 40^\circ = 12^\circ \)
Áp dụng định lí sin trong tam giác BPQ ta có
\(\frac{{PQ}}{{\sin B}} = \frac{{BQ}}{{\sin P}} = \frac{{50}}{{\sin 12^\circ }} \Rightarrow BQ = \frac{{50}}{{\sin 12^\circ }}.\sin P = \frac{{50}}{{\sin 12^\circ }}.\sin 40^\circ \)
Áp dụng định lí sin vào tam giác ABQ ta có:
\(\frac{{BQ}}{{\sin A}} = \frac{{AB}}{{\sin Q}} \Rightarrow AB = \frac{{BQ}}{{\sin A}}.\sin Q = \frac{{\frac{{50}}{{\sin 12^\circ }}.\sin 40^\circ }}{{\sin 90^\circ }}.\sin 52^\circ \simeq 121,81\) (m)
Vậy chiều cao của tháp hải đăng là khoảng 121,81 m
-- Mod Toán 10 HỌC247
Bài tập SGK khác
Giải bài 1 trang 81 SBT Toán 10 Chân trời sáng tạo tập 1 - CTST
Giải bài 2 trang 81 SBT Toán 10 Chân trời sáng tạo tập 1 - CTST
Giải bài 4 trang 81 SBT Toán 10 Chân trời sáng tạo tập 1 - CTST
Giải bài 5 trang 81 SBT Toán 10 Chân trời sáng tạo tập 1 - CTST
Giải bài 6 trang 81 SBT Toán 10 Chân trời sáng tạo tập 1 - CTST
Giải bài 7 trang 81 SBT Toán 10 Chân trời sáng tạo tập 1 - CTST
Chưa có câu hỏi nào. Em hãy trở thành người đầu tiên đặt câu hỏi.