-
Câu hỏi:
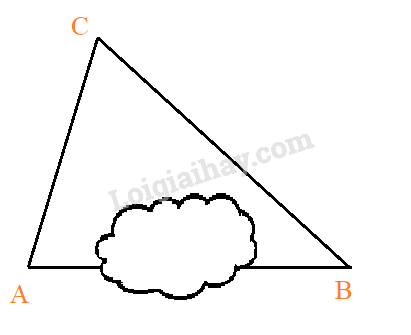
Khoảng cách từ A đến B không thể đo trực tiếp được vì phải qua một đầm lầy. Người ta xác định được một điểm C mà từ đó có thể nhìn được A và B dưới một góc \({60^ \circ }\). Biết \(CA = 200(m),CB = 180(m)\). Khoảng cách AB là?
-
A.
\(168\sqrt 7 (m)\)
-
B.
\(228(m)\)
-
C.
\(20\sqrt {91} (m)\)
-
D.
\(112\sqrt {17} (m)\)
Lời giải tham khảo:
Đáp án đúng: C
Áp dụng định lí cosin trong tam giác ABC ta có:
\(\begin{array}{l}A{B^2} = B{C^2} + A{C^2} - 2BC.AC\cos C\\\quad \quad = {180^2} + {200^2} - 2.180.200.\cos {60^ \circ }\\\quad \quad = 36400\\ \Rightarrow AB = 20\sqrt {91} \end{array}\)
Chọn C.
Hãy trả lời câu hỏi trước khi xem đáp án và lời giải -
A.
Câu hỏi này thuộc đề thi trắc nghiệm dưới đây, bấm vào Bắt đầu thi để làm toàn bài
CÂU HỎI KHÁC
- Mệnh đề nào là phủ định của mệnh đề sau: “\(\exists x \in \mathbb{R}|{x^2} - 3x + 2 > 0\)”?
- Cho tập hợp \(A = \{ 1;2;5;7;8\} \) và \(B = \{ x \in \mathbb{N}|x \le 3\} \). Tìm tập hợp \(A \cap B\)?
- Mỗi HS của lớp 10A đều thích môn Toán hoặc môn Tiếng Anh, biết rằng có 30 học sinh thích môn Toán, 25 học sinh thích môn Tiếng Anh và 15 em học sinh thích cả hai môn. Hỏi lớp 10A có tất cả bao nhiêu học sinh?
- Tính số tập hợp con của tập hợp A có 5 phần tử?
- Cặp số nào sau đây là nghiệm của bpt: \(3(x - 1) + 4(y - 2) < 5x + 3\)?
- GTNN của \(F(x;y) = x - 3y\), với điều kiện \(\left\{ \begin{array}{l}x \ge 0\\0 \le y \le 5\\x + y - 2 \ge 0\\3x - y \le 6\end{array} \right\)?
- Cho \(\cos x = \frac{1}{2}\). Tính giá trị của biểu thức \(P = 5{\sin ^2}x + 1\)?
- Cho biết giá trị của \(T = {\cos ^4}x\;(2{\cos ^2}x - 3) + {\sin ^4}x\;(2{\sin ^2}x - 3)\) là?
- Nếu tam giác ABC có \(\frac{{\sin B}}{{\sin C}} = 2\cos A\) thì...?
- Cho tam giác ABC có \(a = 4,b = 5,c = 7\). Bán kính ĐT ngoại tiếp R của tam giác ABC bằng?
- Cho tam giác \(ABC\) có \(c = 32,\widehat A = {70^o},\widehat C = {45^o}\). Tính độ dài cạnh AC?
- Mệnh đề phủ định của mệnh đề sau “2022 là một số chẵn” là?
- Cho mệnh đề: “Nếu tam giác có hai góc bằng \({60^ \circ }\) thì tam giác đó là tam giác đều”.
- Viết MĐ sau bằng kí hiệu \(\forall \) hoặc \(\exists \): “Có một số nguyên bằng bình phương của chính nó”?
- Hãy viết tập hợp \(A = \{ - 4; - 3; - 2; - 1;0;1;2;3;4\} \) bằng cách chỉ ra tính chất đặc trưng?
- Dùng kí hiệu khoảng, đoạn, nửa khoảng để viết lại tập hợp \(A = \{ x \in \mathbb{R}| - 5 \le x < 3\} \)?
- Kết quả của \(( - 1;4] \cap ( - \infty ;3)\) bằng bao nhiêu?
- Tìm phần bù của \([ - 1;5)\) trong \(\mathbb{R}\)?
- Bất phương trình nào là bpt bậc nhất 2 ẩn?
- Hình vẽ sau là biểu diễn của tập hợp nào?
- Biết \({C_\mathbb{R}}A = [ - 3;11)\) và \({C_\mathbb{R}}B = ( - 8;1]\). Khi đó \({C_\mathbb{R}}\left( {A \cap B} \right)\) bằng?
- Miền không tô màu dưới đây biểu diễn miền nghiệm của bpt nào?
- Miền tam giác ABC kể cả 3 cạnh AB, BC, CA trong hình là miền nghiệm của hệ bpt nào trong 4 hệ bất phương trình sau?
- Chọn khẳng định sai trong các khẳng định dưới?
- Tam giác ABC có \(a = 8,b = 3,B = {60^ \circ }\). Tính độ dài của cạnh \(b\)?
- Cho tam giác ABC có \(B = {30^ \circ },C = {45^ \circ },AB = 3\). Tính cạnh AC?
- Tam giác ABC cân tại A có \(A = {120^ \circ }\). Trong các khẳng định sau, khẳng định đúng là?
- Tam giác ABC có góc A nhọn, AB = 5, AC = 8 và S bằng 12. Tính độ dài cạnh BC?
- Khoảng cách từ A đến B không thể đo trực tiếp được vì phải qua một đầm lầy. Người ta xác định được một điểm C mà từ đó có thể nhìn được A và B dưới một góc \({60^ \circ }\). Biết \(CA = 200(m),CB = 180(m)\). K/c AB là?
- Kí hiệu nào viết đúng về mệnh đề: “\(\sqrt 5 \) không là số nguyên”?
- Trong các mệnh đề sau, MĐ nào là đúng?
- Cho \(A = \{ n = 2k|k \in \mathbb{N},k \le 3\} \) , \(B = \{ n \in \mathbb{N}|n \le 5\} \) và \(C = \{ n \in
- Cho \(A = ( - 2;5]\) và \(B = (m; + \infty )\). Tìm \(m \in \mathbb{Z}\) để \(A{\rm{\backslash }}B\) chứa đúng
- Lớp 10A có 45 học sinh trong đó có 23 em thích môn Văn, 20 em thích môn Toán, 12 em không thích môn
- GTLN của \(F(x;y) = 5x - 3y\), với đk \(\left\{ \begin{array}{l}x \ge 0\\0 \le y \le 5\\x + y - 2 \ge 0\\3x - y \le 6\end{array} \right\)?
- Cho góc \(x\;({0^ \circ } < x < {180^ \circ })\) thỏa mãn \(\tan x = 5\). Tính biểu thức: \(P = \frac{{3\sin x + 11\cos x}}{{7\sin x - 9\cos x}}\)?
- Rút gọn biểu thức sau: \(A = \frac{{\sin x + \sin 3x + \sin 5x}}{{\cos x + \cos 3x + \cos 5x}}\)?
- Cho tam giác ABC. Mệnh đề nào đúng?
- Cho tam giác ABC có \(BC = 5,\widehat {BAC} = {120^o}\). Bán kính ĐT ngoại tiếp \(\Delta ABC\) bằng?
- Cho tam giác \(ABC\) có \(c = 4,b = 7,\widehat A = {60^ \circ }\). Tính chiều cao \({h_a}\) của tam giác ABC (làm tròn đến hàng đơn vị)?


