-
Câu hỏi:
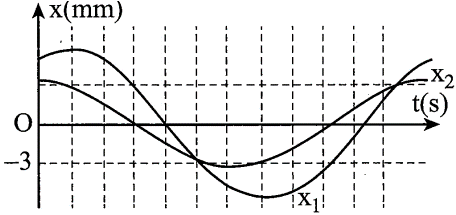
Hai chất điểm M, N dao động điều hòa trên các quỹ đạo song song, gần nhau dọc theo trục Ox, có li độ lần lượt là \({{x}_{1}}\) và \({{x}_{2}}\). Hình bên là đồ thị biểu diễn sự phụ thuộc của \({{x}_{1}}\) và \({{x}_{2}}\) theo thời gian t. Trong quá trình dao động, khoảng cách lớn nhất giữa hai chất điểm xét theo phương Ox là:
-
A.
4,5 mm.
-
B.
5,5 mm.
-
C.
2,5 mm.
-
D.
3,5 mm.
Lời giải tham khảo:
Đáp án đúng: D
Từ đồ thị ta thấy:
Chu kì \(T=12\) đơn vị thời gian.
\({{x}_{1}}\) trễ pha hơn \({{x}_{2}}\) là: \(\frac{1}{12}.2\pi =\frac{\pi }{6}\).
Khoảng cách giữa \({{x}_{1}}\) và \({{x}_{2}}\) theo phương Ox là: \(x={{x}_{1}}-{{x}_{2}}=A\cos \left( \omega t+\varphi \right)\).
\(\Rightarrow \)Khoảng cách này lớn nhất bằng \({{X}_{\max }}=A=\sqrt{A_{1}^{2}+A_{2}^{2}-2{{A}_{1}}{{A}_{2}}.\cos \Delta \varphi }\).
Tại \(t=5\) đơn vị thời gian thì cả hai vật đều có li độ là \(-3cm\).
Ban đầu \({{x}_{2}}\) cực đại, nên pha ban đầu của \({{x}_{2}}\) là: \({{\varphi }_{02}}=0\).
\({{x}_{2}}={{A}_{2}}\cos \left( \frac{2\pi }{12}.5+0 \right)=-3\Rightarrow {{A}_{2}}=2\sqrt{3}cm\).
Từ vị trí ban đầu của \({{x}_{1}}\) xác định được pha ban đầu của là: \({{\varphi }_{01}}=-\frac{1}{12}.2\pi =-\frac{\pi }{6}\).
\({{x}_{1}}={{A}_{1}}\cos \left( \frac{2\pi }{12}.5-\frac{\pi }{6} \right)=-3\Rightarrow {{A}_{1}}=6cm\).
Khoảng cách giữa \({{x}_{1}}\) và \({{x}_{2}}\) lớn nhất bằng:
\({{X}_{\max }}=A=\sqrt{A_{1}^{2}+A_{2}^{2}-2{{A}_{1}}{{A}_{2}}.\cos \Delta \varphi }=\sqrt{{{6}^{2}}+{{\left( 2\sqrt{3} \right)}^{2}}-2.6.2\sqrt{3}.\cos \frac{\pi }{6}}=3,464cm\).
Hãy trả lời câu hỏi trước khi xem đáp án và lời giải -
A.
Câu hỏi này thuộc đề thi trắc nghiệm dưới đây, bấm vào Bắt đầu thi để làm toàn bài
CÂU HỎI KHÁC
- Quạt cây sử dụng trong nhà có cánh quạt được gắn với trục quay
- Sóng điện từ lan truyền trong không gian, tại một điểm dđ của điện trường
- Một kim loại có công thoát electron là A. Biết hằng số Plăng là h
- Chọn phát biểu đúng. Tia hồng ngoại:
- Trong pt dđ điều hòa: \(x=A\cos \left( \omega t+\varphi \right)\)
- Hạt nhân \(_{Z}^{A}X\) có số prôtôn là:
- Tính cường độ điện trường do một điện tích điểm \(Q=+{{4.10}^{-9}}C\)
- Hiện tượng hai sóng trên mặt nước gặp nhau tạo nên các gợn sóng ổn định
- Một vật dđ đh theo pt \(x=A\cos \left( \omega t+\varphi \right)\left( A>0,\omega >0 \right)\)
- Trong máy phát điện xc một pha, phần cảm có p cặp cực, quay với tốc độ n
- Chiếu chùm ánh sáng gồm 5 ánh sáng đơn sắc khác nhau là đỏ, cam, vàng, lục
- Mạch dao động gồm một tụ điện có điện dung \(10\mu F\) và 1 cuộn dây thuần
- Trong 1 tn Y-âng về giao thoa ás, khoảng cách giữa hai khe là\(a=0,5\ mm\)
- Cho mạch điện như hình vẽ. Biết \(E=12\ V,r=4\Omega \)
- Hạt nhân nào có thể phân hạch:
- Độ to là một đặc tính sinh lí của âm phụ thuộc vào:
- Khi nói về tính chất của tia tử ngoại, phát biểu nào là sai?
- Một con lắc đơn có chiều dài 160 cm, dđ điều hòa với biên độ dài 16 cm.
- Cho một đoạn mạch RC có \(R=50\Omega ,C=\frac{{{2.10}^{-4}}}{\pi }F\).
- Hai sóng chạy có vận tốc 750 m/s,truyền ngược chiều nhau và giao thoa nhau
- Đặt điện áp xc vào hai đầu đoạn mạch có R, L, C mắc nối tiếp.
- Xét nguyên tử hiđrô theo mẫu nguyên tử Bo. Biết bán kính Bo là \({{r}_{0}}\)
- Một vật dđ đh pt \(x=10\cos \left( 10\pi t+\frac{\pi }{3} \right)cm\).
- Một chất điểm dao động điều hòa theo phương trình \(x=2\cos 2\pi t\ cm\)
- Đặt điện áp xoay chiều có giá trị cực đại là 200 V vào hai đầu một tụ điện
- Dao động được ứng dụng trong thiết bị giảm xóc của ô tô là:
- Trên 1 sợi dây dài đang có sóng ngang hình sin truyền qua theo chiều dương
- Vật sáng AB đặt trước một TKHT cho ảnh rõ nét trên màn cách vật 90 cm.
- Thực hiện thí nghiệm Y-âng giao thoa ánh sáng, hai khe hẹp cách nhau 1 mm
- Dao động của một chất điểm là tổng hợp của hai dđ điều hòa cùng phương
- 1 đám nguyên tử hiđrô đang ở trạng thái kích thích mà êlectron chuyển động
- Một cuộn dây tròn có 100 vòng dây, mỗi vòng dây có bán kính \(R=2,5\ cm\)
- 1 vật thực hiện đồng thời 2 dao động điều hòa cùng phương cùng tần số
- Đặt điện áp là \(u={{U}_{0}}\cos \left( 100\pi t+\frac{\pi }{3} \right)V\)
- Kim loại có công thoát êlectron là 2,62 eV
- Trong thí nghiệm Y-âng về giao thoa ás, hai khe \({{S}_{1}},{{S}_{2}}\)
- Một sợi dây đàn hồi dài 60 cm có một đầu cố định
- Đoạn mạch AB gồm điện trở \(R=50\ \Omega \), cuộn dây có độ tự cảm
- Dao động điện từ trong mạch dao động LC lí tưởng (gồm cuộn dây thuần cảm
- Hai chất điểm M, N dđ điều hòa trên các quỹ đạo song song, gần nhau dọc theo trục Ox

