-
Câu hỏi:
Cho tam giác ABC vuông tại A, đường cao AH. Cho biết AB : AC = 3 : 7 và AH = 42cm. Tính độ dài CH?
-
A.
CH = 96
-
B.
CH = 98
-
C.
CH = 49
-
D.
CH = 89
Lời giải tham khảo:
Đáp án đúng: B
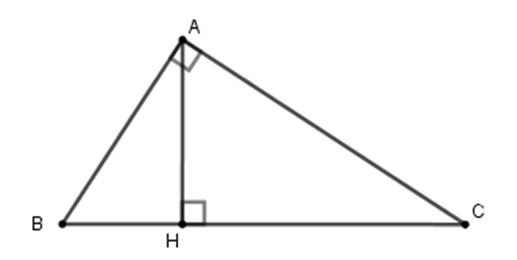
Ta có: AB : AC = 3 : 7, đặt AB = 3a; AC = 7a (a > 0)
Theo hệ thức lượng:
\(\begin{array}{*{20}{l}}
{\frac{1}{{A{H^2}}} = \frac{1}{{A{B^2}}} + \frac{1}{{A{C^2}}} \Rightarrow \frac{1}{{42}} = \frac{1}{{9{a^2}}} + \frac{1}{{{{49}^2}}} \Rightarrow \frac{1}{{1764}} = \frac{{58}}{{441{a^2}}}}\\
{ \Rightarrow 441{a^2} = 102312 \Rightarrow A = 2\sqrt {58} (TM) \Rightarrow AB = 6\sqrt {58} ;AC = 14\sqrt {58} }
\end{array}\)Theo định lý Py-ta-go cho tam giác vuông AHC ta có:
\(CH = \sqrt {A{C^2} - A{H^2}} = \sqrt {{{(14\sqrt {58} )}^2} - {{42}^2}} = 98\)
Chọn đáp án B.
Hãy trả lời câu hỏi trước khi xem đáp án và lời giải -
A.
Câu hỏi này thuộc đề thi trắc nghiệm dưới đây, bấm vào Bắt đầu thi để làm toàn bài
CÂU HỎI KHÁC
- Đẳng thức nào dưới đây đúng nếu x là số âm?
- Tính giá trị của \(\sqrt {\dfrac{{49}}{{0,09}}}\)
- Cho biết giá trị của \(\sqrt {1,6} .\sqrt {2,5}\)?
- Tra bảng căn bậc hai, tìm \(\sqrt {35,92} \) được \(\sqrt {35,92} \approx 5,993\). Vậy \(\sqrt {0,3592} \) có giá trị gần đúng?
- Tìm giá trị của \(\sqrt {0,16} \)?
- Tìm giá trị của x để \(\sqrt {\frac{{ - 2}}{{3x - 1}}}\) có nghĩa
- Tính giá trị biểu thức sau: \(9\sqrt {{{\left( { - \frac{8}{3}} \right)}^2}} + \sqrt {{{\left( { - 0,8} \right)}^2}} \)?
- Rút ngọn biểu thức sau: A = \(\sqrt {144{a^2}} - 9a\) với a > 0?
- Tìm điều kiện xác định của biểu thức\(\sqrt {5 - 3x}\)?
- Biểu thức sau \(\mathrm{B}=\frac{2}{\sqrt{1-3 x}}\) xác định khi nào?
- Rút gọn biểu thức sau \(3\sqrt {{x^2}y} + x\sqrt y \) với \(x < 0,y \ge 0\)
- Cho tam giác \(ABC\) vuông tại \(A\) có \(AB : AC = 3 : 4\) và đường cao \(AH\) bằng 9cm. Tinh độ dài đoạn thẳng \(HC\)?
- Với \(x < 0; y < 0\) biểu thức \(x\sqrt {\dfrac{x}{{{y^3}}}} \) được biến đổi thành?
- Cho tam giác \(ABC\) vuông tại \(A\) có \(AB : AC = 4 : 5\) và đường cao \(AH\) bằng \(12cm\). Tìm độ dài đoạn thẳng \(HB\)?
- Tính giá trị của biểu thức \(\dfrac{6}{{\sqrt 7 - 1}}\)
- Cho tam giác ABC vuông tại A, đường cao AH. Cho biết AB : AC = 3 : 7 và AH = 42cm. Tính độ dài CH?
- Tìm giá trị của biểu thức \(E=\sqrt{(\sqrt{3}+1)^{2}}\)
- Cho tam giác ABC vuông tại A, đường cao AH có AB = 12cm, BH = 8cm. Tính diện tích tam giác ABC?
- Tìm giá trị xác định của biểu thức \(D=\sqrt{-x^{2}+7 x-12}\)
- Rút gọn biểu thức \(A=\sqrt{11+6 \sqrt{2}}\) ta được
- Tam giác vuông có hai cạnh góc vuông là \(a,\, b;\) góc đối diện với cạnh \(a\) là \(α ;\) góc đối diện với cạnh \(b\) là \(β\) và cạnh huyền là \(c.\) Tìm khẳng định đúng?
- Căn bậc hai của \(25\) bằng?
- Giá trị của x trong hình bằng?
- Khẳng định nào dưới đây đúng?
- Căn bậc hai số học của số \(36\) là bao nhiêu?
- Đẳng thức nào bên dưới đúng nếu x là số âm?
- Tính giá trị của \(\sqrt {5,{5^2}{\rm{ }} - {\rm{ }}3,{5^2}{\rm{ }}} \)
- Rút gọn biểu thức: \( T = (1 + cos\alpha )(1 - cos\alpha ) - ta{n^2}\alpha + si{n^2}\alpha .ta{n^2}\alpha \)
- Tìm giá trị của biểu thức \(\sqrt {5x + 3} .\sqrt {5x - 3} \) khi \(x = \sqrt {3,6} \)
- Thang AB dài 6,7m tựa vào tường làm thành góc \(63^0\) với mặt đất. Hỏi chiều cao của thang?
- Để vẽ 1 tam giác cân có góc ở đáy là \(50^0\) mà không có thước đo góc, 1 học sinh vẽ tam giác cân có cạnh bên 3cm, cạnh đáy 4cm. Tính góc ở đáy của hình đó?
- Cho tam giác ABC vuông tại A. Tính giá trị \( A = {\sin ^2}B + {\sin ^2}C - \tan B.\tan C\)?
- Cho hai góc nhọn \(\alpha \) và \(\beta \) phụ nhau. Khi đó...?
- Biến đổi biểu thức: \(2\sqrt {{x^2}y} + x\sqrt y \) với \(x < 0,\,\,y \ge 0\) được?
- Tính giá trị của \(\dfrac{2}{{\sqrt 3 + 1}}\) được?
- Tính giá trị của \(\dfrac{1}{{\sqrt 3 - \sqrt 2 }} - \dfrac{1}{{\sqrt 3 + \sqrt 2 }}\) được?
- Một cây tre cao 9m bị gió bão làm gãy ngang thân cây, ngọn cây chạm đất cách gốc 3m. Hỏi chỗ gãy cách gốc bao nhiêu? (làm tròn đến chữ số thập phân thứ hai).
- Rút gọn biểu thức: \( \left( {15\sqrt {200} - 3\sqrt {450} + 2\sqrt {50} } \right):\sqrt {10}\)?
- Đưa thừa số \( \sqrt {144{{\left( {3 + 2a} \right)}^4}} \) ra ngoài dấu căn ta được giá trị?
- So sánh \(5\sqrt3\) và \(4\sqrt5\)?

