-
Câu hỏi:
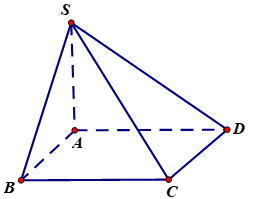
Cho hình chóp \(S.ABCD\) có đáy là hình vuông \(ABCD\) cạnh \(a\). Cạnh \(SA=a\sqrt{3}\) và vuông góc với đáy. Góc giữa đường thẳng \(S\text{D}\)và mặt phẳng đáy bằng
-
A.
\({{30}^{0}}\).
-
B.
\({{90}^{0}}\).
-
C.
\({{45}^{0}}\).
-
D.
\({{60}^{0}}\).
Lời giải tham khảo:
Đáp án đúng: D
Chọn D
Do \(SA\)vuông góc với \((ABC\text{D})\)nên \(AD\)là hình chiếu của \(SD\)lên mặt phẳng \((ABC\text{D})\).
Vậy góc giữa \(SD\)và \((ABC\text{D})\)là góc giữa \(SD\)và \(AD\) chính là góc \(\widehat{SDA}\).
Xét tam giác \(SAD\)vuông tại \(A\)và có \(SA=a\sqrt{3};AD=a\Rightarrow \tan \widehat{SDA}=\frac{SA}{AD}=\sqrt{3}\Rightarrow \widehat{SDA}=60{}^\circ \Rightarrow (SD,(ABCD))={{60}^{0}}\).
Hãy trả lời câu hỏi trước khi xem đáp án và lời giải -
A.
Câu hỏi này thuộc đề thi trắc nghiệm dưới đây, bấm vào Bắt đầu thi để làm toàn bài
QUẢNG CÁO
CÂU HỎI KHÁC
- Cho hình chóp \(S.ABC\) có \(SA\bot \left( ABC \right)\); tam giác \(ABC\) đều cạnh \(a\) và \(SA=a\).
- Cho hình chóp \(S.ABC\)có đáy là tam giác đều \(ABC\) cạnh bằng \(a\) và \(SC\bot \left( ABC \right)\).
- Trong không gian mệnh đề nào sau đây đúng: Góc giữa đường thẳng và mặt phẳng bằng góc giữa đường thẳng đó và hình chiếu của nó trên mặt phẳng đã cho
- Cho hình chóp \(S.ABCD\)có đáy \(ABCD\)là hình vuông cạnh \(a\), \(SA\bot \left( ABCD \right)\)và \(SA=a\sqrt{3}\)
- Cho hình chóp \(S.ABCD\) có đáy là hình thoi tâm \(O\), \(SO\) vuông góc với mặt phẳng đáy
- Cho hình chóp \(S.ABCD\) có đáy là hình vuông \(ABCD\) cạnh \(a\).
- Cho hình chóp \(S.ABCD\), với đáy \(ABCD\) là hình vuông cạnh bằng \(a\) và \(SA\bot \left( ABCD \right)\).
- Cho hình chóp \(S.ABCD\)có đáy \(ABCD\)là hình vuông cạnh \(2a\), \(SA=SB=SC=SD=2a.\)
- Cho hình chóp \(S.ABC\) có \(SA\bot \left( ABC \right)\), \(SA=a\sqrt{3}\). Tam giác \(ABC\) đều cạnh \(a\).
- Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình vuông cạnh \(a\),\(SA=a\sqrt{2}\)
VIDEO
YOMEDIA
ADMICRO
