-
Câu hỏi:
Cho hàm số \(f\left( x \right)=\,{{x}^{4}}+2{{x}^{2}}+1\). Có bao nhiêu giá trị nguyên của tham số \(m\in \left[ 0\,;\,10 \right]\) để hàm số \(g\left( x \right)=f\left( 3\left| x-m \right|+{{m}^{2}} \right)\) nghịch biến trên khoảng \(\left( -\infty \,;\,1 \right)\)?
-
A.
11
-
B.
5
-
C.
10
-
D.
9
Lời giải tham khảo:
Đáp án đúng: C
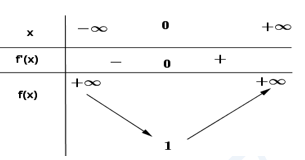
Xét hàm số \(f\left( x \right)=\,{{x}^{4}}+2{{x}^{2}}+1\)
Ta có \({f}'\left( x \right)=4{{x}^{3}}+4x\); \({f}'\left( x \right)=0\Leftrightarrow x=0\)
Bảng biến thiên
Ta có \({g}'\left( x \right)={f}'\left( 3\left| x-m \right|+{{m}^{2}} \right).{{\left( 3\left| x-m \right|+{{m}^{2}} \right)}^{\prime }}\) =\({f}'\left( 3\left| x-m \right|+{{m}^{2}} \right).\frac{3\left( x-m \right)}{\left| x-m \right|}\).
\({g}'\left( x \right)=0\) \(\Leftrightarrow \left[ \begin{align} & x-m=0\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\left( 1 \right) \\ & 3\left| x-m \right|+{{m}^{2}}=0\,\,\,\left( 2 \right) \\ \end{align} \right.\)
TH1: Nếu \(m=0\) \(\Rightarrow \) phương trình \({g}'\left( x \right)=0\Leftrightarrow x=0\)\(\Rightarrow \) không thỏa mãn nghịch biến trên khoảng \(\left( -\infty \,;\,1 \right)\) nên trường hợp này bị loại.
TH2: Nếu \(m>0\) \(\Rightarrow \) phương trình \({g}'\left( x \right)=0\Leftrightarrow x=m\)
Ta có \(3\left| x-m \right|+{{m}^{2}}>0\,\,\forall x<1\)\(\Rightarrow {f}'\left( 3\left| x-m \right|+{{m}^{2}} \right)>0\,\,\forall \,x\in \left( -\infty \,;\,1 \right)\) nên \({g}'\left( x \right) < 0\)\( \Leftrightarrow x < m\).
\(\Rightarrow \) hàm số \(y=g\left( x \right)\) nghịch biến trên \(\left( -\infty \,;\,1 \right)\)\(\Leftrightarrow {g}'\left( x \right)<0\,\forall \,x\in \left( -\infty \,;\,1 \right)\)
\(\Leftrightarrow \,\left( -\infty \,;\,1 \right)\subset \left( -\infty \,;\,m \right)\Leftrightarrow 1\le m\)\(\Rightarrow m\in \left\{ 1;2;3;4\,;5;6;7;8;9;10 \right\}\). Nên có 10 giá trị thỏa mãn.
Chọn C
Hãy trả lời câu hỏi trước khi xem đáp án và lời giải -
A.
Câu hỏi này thuộc đề thi trắc nghiệm dưới đây, bấm vào Bắt đầu thi để làm toàn bài
CÂU HỎI KHÁC
- Cho tập hợp \(A\) có \(7\) phần tử. Cho biết số tập con có \(3\) phần tử của tập \(A\) là?
- Trong không gian \(Oxyz\), cho đường thẳng \(d:\frac{x-1}{2}=\frac{y+1}{-1}=\frac{z+3}{2}\). Trong các vectơ dưới đây, vectơ nào là vectơ chỉ phương của đường thẳng \(d\)?
- Cho số phức \(z=\frac{5}{2}-\frac{1}{2}i\). Tìm tọa độ điểm \(M\) biểu diễn số phức \(z\) là?
- Hàm số nào có đồ thị như đường cong trong hình bên?
- Cho hàm số \(y=f\left( x \right)\) có BBT như sau: Hàm số đã cho đồng biến trên khoảng nào?
- Một hình nón có bán kính đáy bằng \(3\), đường sinh bằng \(5\). Diện tích xung quanh Sxq của hình nón là?
- Cho hàm số \(y=f\left( x \right)\) có BBT như sau: Có bao nhiêu giá trị nguyên dương \(m\) để phương trình \(3f\left( x \right)+2m=0\) có \(2\) nghiệm thực phân biệt?
- Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình vuông cạnh \(a\), cạnh bên \(SA=2a\) và vuông góc với mp đáy. Thể tích khối chóp \(S.ABCD\) bằng?
- Nghiệm của bất phương trình sau đây \({{\log }_{2}}x>1\) là?
- Trong không gian \(Oxyz\), mp \(\left( Oxz \right)\) có phương trình là?
- Tính đạo hàm của hàm số sau đây \(y={{3}^{2x+1}}\)?
- Nguyên hàm của hàm số sau đây \(f(x)={{3}^{x}}-x\) là?
- TXĐ của hàm số \(y={{\left( {{x}^{2}}-x-2 \right)}^{-10}}\) là?
- Tính thể tích \(V\) của khối lăng trụ tứ giác đều có chiều cao bằng \(3cm\), cạnh đáy bằng \(5cm\) là?
- Một CSC \(\left( {{u}_{n}} \right)\) có \({{u}_{13}}=8\) và công sai \(d=-3.\) Tìm số hạng thứ 3 của cấp số cộng \(\left( {{u}_{n}} \right)\)?
- Cho 2 tích phân \({\int\limits_{2}^{5}{f\left( x \right)\text{d}x}=8}\) và \({\int\limits_{2}^{5}{g\left( x \right)\text{d}x}=3}\). Tính\({I=\int\limits_{2}^{5}{\left[ f\left( x \right)-g\left( x \right) \right]\text{d}x}}\)?
- Cho hàm số \(f\left( x \right)\) liên tục trên tập \(\mathbb{R}\) thỏa mãn \(\int\limits_{0}^{1}{f\left( 2x \right)\text{d}x}=-5\). Tính tích phân sau \(I=\int\limits_{0}^{2}{f\left( x \right)\text{d}x}\)?
- Tìm tất cả các giá trị của tham số \(m\) để hàm số \(y=-{{x}^{4}}+\left( m-5 \right){{x}^{2}}+4\) có 3 điểm cực trị?
- Trong không gian với hệ toạ độ \(Oxyz\), cho điểm \(M\left( 2;-3;1 \right)\) và mp \(\left( \alpha \right):x+3y-z+2=0\). Đường thẳng \(d\) đi qua điểm \(M\) và vuông góc với mặt phẳng \(\left( \alpha \right)\) có phương trình là?
- Số đường tiệm cận của ĐTHS \(y=\frac{x}{x-1}\) là?
- Cho \(a,b,c\) là các số dương khác \(1\) thoả mãn \({{\log }_{a}}b=2,\,{{\log }_{b}}c=3\). Tính giá trị của \({{\log }_{c}}a\)?
- Tìm mặt phẳng chứa \(\left( \Delta \right)\) và song song với \(AB\) có phương trình là?
- Họ nguyên hàm của hàm số sau đây \(f\left( x \right)=3{{x}^{2}}-\frac{1}{x}+\frac{2}{{{x}^{2}}}\) là?
- Cho số phức \(z\) thỏa mãn rằng \(3z+2\overline{z}={{\left( 4-i \right)}^{2}}\). Mô đun của số phức \(z\) là?
- Trong mặt phẳng tọa độ \(O\,xy,\,\) tập hợp các điểm biểu diễn số phức \(z\) thỏa mãn \(3+\overline{iz}\) là số thuần ảo, là 1 đường thẳng có phương trình?
- Xét tích phân sau đây \(I=\int\limits_{\frac{\pi }{3}}^{\frac{\pi }{2}}{\frac{\sin 2x}{1+\cos x}dx}\). Nếu đặt \(t=\cos x\) thì tích phân \(I\) trở thành?
- Xếp ngẫu nhiên \(6\) học sinh nam và \(4\) học sinh nữ quanh 1 bàn tròn. Xác suất để các học sinh nữ luôn ngồi cạnh nhau là?
- Số nghiệm thực phân biệt của phương trình sau đây \({{5}^{{{x}^{2}}}}{{3}^{{{x}^{2}}+1}}=1\) là?
- Cho hàm số \(y=\frac{x+a}{bx+c}\) có đồ thị như hình dưới: Khẳng định nào đúng?
- Với \(a\) là số thực dương tuỳ ý, giá trị của \(\log \left( \frac{10}{{{a}^{2}}} \right)\) bằng?
- Cho hình chóp \(S.ABCD\) có đáy là hình chữ nhật, biết \(BC=2a\) và \(SA\) vuông góc với mặt phẳng đáy. K/c từ \(D\) đến mặt phẳng \(\left( SAB \right)\) bằng?
- Cho hình nón đỉnh \(S\) có bán kính đáy bằng \(5a\). Gọi \(A\) và \(B\) là 2 điểm thuộc đường tròn đáy sao cho \(AB=8a\). Biết mặt phẳng \(\left( SAB \right)\) tạo với đáy một góc \({{60}^{0}}\), diện tích xung quanh \(S\) của hình nón đã cho bằng?
- Trong không gian với hệ trục tọa độ \(Oxyz,\) cho điểm \(A\left( 1\,;\,1\,;\,2 \right)\), \(B\left(
- Thể tích khối tròn xoay tạo thành khi quay quanh trục hoành hình phẳng giới hạn bởi các đường thẳng \(y={{x}^{3}}\) & \(y=2{{x}^{2}}\) là?
- Cho hình lập phương \(ABCD.{A}'{B}'{C}'{D}'\). Góc giữa 2 đường thẳng \(B{A}'\) và \({B}'{D}'\) bằng?
- Có bao nhiêu giá trị thực của tham số \(m\) để phương trình sau \(4{{z}^{2}}+4\left( m-1 \right)z+{{m}^{2}}-3m=0\) có 2 nghiệm phức \({{z}_{1}}\), \({{z}_{2}}\) thỏa mãn \(\left| {{z}_{1}} \right|+\left| {{z}_{2}} \right|=\sqrt{10}\)?
- Cho hàm số \(y=\,f(x)=\,a{{x}^{3}}+b{{x}^{2}}+cx+d,\,\) \((a,\,b,\,c,\,d\,\in \mathbb{R},\,a\ne \,0)\). Biết đồ
- Trong không gian cho mặt cầu \(\left( S \right):{{\left( x-1 \right)}^{2}}+{{y}^{2}}+{{\left( z-4
- Trong không gian \(Oxyz\), cho 2 đường thẳng \({{d}_{1}}:\frac{x-1}{2}=\frac{y}{1}=\frac{z+2}{-1}\) và \({{d}_{2}}:\frac{x-1}{1}=\frac{y+2}{3}=\frac{z-2}{-2}\). Gọi \(\Delta \) là đường thẳng song song với mặt phẳng \(\left( P \right):x+y+z-7=0\) và cắt \({{d}_{1}},\,{{d}_{2}}\) lần lượt tại hai điểm \(A,\,B\) sao cho \(AB\) ngắn nhất. phương trình của đường thẳng \(\Delta \) là?
- Cho hình lăng trụ đứng \(ABC.{A}'{B}'{C}'\) có đáy là tam giác đều cạnh \(a.\) Góc giữa đường thẳng \(A{B}'\) và mặt phẳng \(\left( BC{C}'{B}' \right)\) bằng \(30{}^\circ \). Gọi \(M,N\) lần lượt là trung điểm của các cạnh \(AB\) và \({B}'{C}'\). Mặt phẳng \(\left( {A}'MN \right)\) cắt \(BC\) tại \(P\). Thể tích khối đa diện \(MBP.{A}'{B}'N\) bằng?
- Cho hàm số \(f\left( x \right)\) có đạo hàm và đồng biến trên \(\left[ 1;4 \right],\) thoả mãn \(x+2xf\left( x \right)={{\left[ f'\left( x \right) \right]}^{2}}\) với mọi \(x\in \left[ 1;4 \right].\) Biết rằng \(f\left( 1 \right)=\frac{3}{2},\) tính tích phân của \(I=\int\limits_{1}^{4}{f\left( x \right)}dx\)?
- Cho hàm số \(f\left( x \right)\) thỏa mãn \(f\left( 0 \right)=\frac{2}{3}\) và \(\left( \sqrt{x}+\sqrt{x+1}
- Số giá trị nguyên nhỏ hơn \(2020\) của tham số \(m\) để phương trình sau \({{{\log }_{6}}\left( 2020x+m \right)={{\log }_{4}}\left( 1010x \right)}\) có nghiệm là?
- Cho hàm số \(f\left( x \right)\) liên tục trên \(\mathbb{R}\) và có BBT như sau: Số nghiệm thuộc khoảng \(\left( -\infty ;\ln 2 \right)\) của phương trình \(2020f\left( 1-{{e}^{x}} \right)-2021=0\) là?
- Cho hàm số \(f\left( x \right)=\,{{x}^{4}}+2{{x}^{2}}+1\). Có bao nhiêu giá trị nguyên của tham số \(m\in \left[ 0\,;\,10 \right]\) để hàm số \(g\left( x \right)=f\left( 3\left| x-m \right|+{{m}^{2}} \right)\) nghịch biến trên khoảng \(\left( -\infty \,;\,1 \right)\)?
- Có tất cả bao nhiêu cặp số nguyên dương \(\left( x;y \right)\) thỏa mãn điều kiện \(x\le 2022\) và \(3\left( {{9}^{y}}+2y \right)+2\le x+{{\log }_{3}}{{\left( x+1 \right)}^{3}}\)?
- Có bao nhiêu số nguyên dương \(y\) nhỏ hơn \(500\) sao cho ứng với mỗi \(y\) tồn tại ít nhất 9 số nguyên \(x\) thỏa mãn bất phương trình sau \({{x}^{4}}+2{{x}^{2}}-y+1\le {{\log }_{2}}\frac{\sqrt{2y+1}}{{{x}^{2}}+1}\)?
- Cho hàm số \(y=f(x)\) có đạo hàm là \({f}'(x)=(2-x){{\left( {{x}^{3}}-{{x}^{2}}-m \right)}^{2021}},\forall x\in \mathbb{R}\). Có bao nhiêu giá trị nguyên thuộc khoảng \((-2021 ; 2022)\) của tham số \(\mathrm{m}\) để hàm số \(g(x)=f\left(x^{2}-2\right)+\frac{1}{2} x^{4}-4 x^{2}+2022\) có đúng 5 điểm cực trị?
- Cho hàm số \(f\left( x \right)\) thỏa mãn \(f'\left( x \right)=\left( 2x+1 \right){{e}^{x-f\left( x \right)}}\)
- Xét các số phức \(w,{{z}_{1}},{{z}_{2}}\) thỏa mãn \(\left| {{z}_{1}}+1+2i \right|+\left| {{z}_{1}}-5-6i